Recomendações aos alunos:
* Leiam com atenção e observem os exemplos.
* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.
* Façam pesquisas em livros didáticos ou pela internet.
* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível)
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 22/09.
Olá pessoal! Que todos estejam bem.
Vamos continuar o estudo de interações gravitacionais.
Já vimos as Leis de Kepler ( lei das órbitas, lei das áreas e a lei dos períodos ), a Lei de Gravitação Universal de Isaac Newton ( F = G . M . m/d² ).
E a aplicação da Lei da Gravitação Universal em movimentos próximos à superfície terrestre e sem a resistência do ar (queda livre).
Para lançamentos verticais e horizontais, próximos da superfície terrestre, valem as equações de Galileu do movimento uniformemente variado e a equação de Torricelli.
Lembrando, que:
Movimento uniformemente variado (M.U.V.) é todo movimento que possui aceleração constante.
A aceleração é a grandeza que provoca variação na velocidade. Pode ser positiva (aumenta a velocidade ) ou negativa (diminui a velocidade).
Equações de Galileu do M.U.V.
* Função horária das velocidades: V = V₀ + a . t , responde questões relacionadas a velocidade do corpo.
* Função horária das posições: S = S₀ + V₀.t + a/2 . t² , responde questões relacionadas a posição do corpo
* Equação de Torricelli: V² = V₀² + 2 . a . ΔS , é a junção das duas equações de Galileu.
Onde:
V = velocidade final (m/s)
V₀ = velocidade inicial (m/s)
a = aceleração ( m/s²)
t = tempo (s)
S = posição final (m)
S₀ = posição inicial (m)
ΔS = distância percorrida (m)
ΔS = S - S₀
A equação de Torricelli é a junção das duas equações de Galileu. Com ela, respondemos questões relacionadas a velocidade e a posição de um objeto, sem a necessidade de saber o tempo.
Quando estudamos corpos em queda livre, a aceleração (a) é substituída pela aceleração da gravidade local (g). E como já vimos, g = 9,8 m/s², ao nível do mar e numa latitude de 45°.
A força com que um planeta atraí os objetos para o seu centro, é o peso do objeto.
O peso é o produto da massa pela aceleração da gravidade local ( P = m .g ), e sua unidade de medida é o newton (N).
Quando um corpo é lançado verticalmente para cima com uma velocidade, ele sobe até parar. Nesse momento o corpo atinge a altura máxima
Durante a subida, o movimento é retardado,ou seja, a aceleração é negativa. Durante a descida, o movimento é acelerado, ou seja, aceleração positiva.
As Leis de Kepler.
1ª Lei de Kepler - Lei das Órbitas
Os planetas descrevem órbitas elipticas em torno do Sol, que ocupa um dos focos da elipse.
2ª Lei de Kepler - Lei das Áreas
O segmento que une o sol a um planeta descreve áreas iguais em intervalos de tempo iguais.
3ª Lei de Kepler - Lei dos Períodos
O quociente dos quadrados dos períodos e o cubo de suas distâncias médias do sol é igual a uma constante k, igual a todos os planetas.
Tendo em vista que o movimento de translação de um planeta é equivalente ao tempo que este demora para percorrer uma volta em torno do Sol, é fácil concluirmos que, quanto mais longe o planeta estiver do Sol, mais longo será seu período de translação e, em consequência disso, maior será o "seu ano".
No estudo de astronomia muitas vezes as unidades do Sistema Internacional (SI) são ineficientes pois as distâncias que devem ser expressas são muito grandes.
Por exemplo: A distância da Terra até Marte é de cerca de 75 milhões de quilômetros, que no SI é expresso por 75 000 000 000 metros.
Devido à necessidade de unidades mais eficientes são utilizadas: Unidade Astronômica (UA), Anos-luz (AL) e Parsec (Pc).
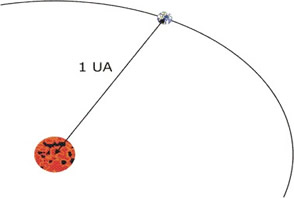
Unidade Astronômica (UA)
É a distância média entre a Terra e o Sol. É empregada principalmente para descrever órbitas e distâncias dentro do Sistema Solar.
![]()
O tamanho médio da órbita dos planetas do Sistema Solar, ou seja, sua distância ao Sol é:
Planeta | Distância ao Sol (UA) |
Mercúrio | 0,39 |
Vênus | 0,72 |
Terra | 1,00 |
Marte | 1,52 |
Júpter | 5,20 |
Saturno | 9,53 |
Urano | 19,10 |
Netuno | 30,00 |
Ano-Luz (al)
É a distância percorrida pela luz, no vácuo, no tempo de 1 ano terrestre.
Sendo a velocidade da luz c = 299 792,458 km/s, temos que:
1 al = 9 460 536 207 068 016 m = 63241,07710 UA
A estrela mais próxima do Sol é chamada Próxima Centauri, localizada na constelação de Centauro. A sua distância ao Sol é de 4,22 al
Parsec (Pc)
É a distância na qual 1 UA é representada por 1'' (1 segundo de arco), em uma medição por paralaxe.
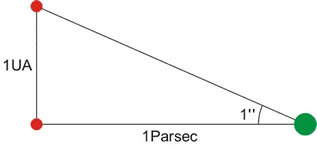
Esta unidade é usada para distância muito grandes, como a distância entre estrelas, entre galáxias ou de objetos muito distantes, como quasares.
![]()
Quando um objeto é lançado para cima, ele sobe até um limite de velocidade, para momentaneamente e, logo depois, inicia o movimento de queda. No entanto, existe um valor determinado de velocidade em que o objeto não volta mais para Terra e simplesmente sai em direção ao espaço sideral. Essa velocidade mínima para sair de um corpo celeste é denominada de velocidade de escape.
A velocidade de escape relaciona-se com a massa (M) do planeta ou estrela de onde se quer escapar, com o raio (R) desse planeta e com a constante de gravitação universal (G), que possui valor de 6,67 x 10 -11 N.m2/kg2. A equação abaixo determina a velocidade de escape:
Repare que essa equação não depende da massa do corpo a ser lançado para fora do planeta ou estrela. Assim, para um corpo muito ou pouco massivo, a velocidade de escape será a mesma. A tabela abaixo indica a velocidade de escape para alguns corpos celestes:
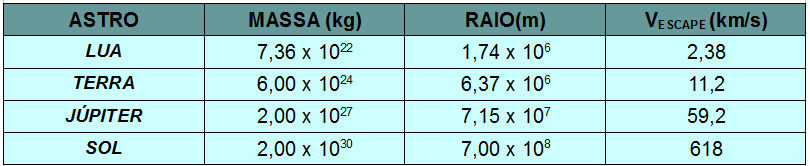
A velocidade de escape também não depende da direção em que o corpo será lançado, mas existem situações em que o lançamento de objetos para o espaço pode ser feito de forma mais fácil. Próximo à linha do equador, a velocidade de rotação da Terra é a maior possível, o que faz com que o objeto a ser lançado ganhe energia extra. Além disso, o lançamento deve ser feito preferencialmente na direção leste, acompanhando o movimento de rotação da Terra.
Os buracos negros são elementos extremamente massivos que possuem velocidade de escape maior que a velocidade da luz. Por essa razão, nem mesmo a própria luz, ao entrar em um buraco negro, consegue escapar dele.
Por Joab Silas
Graduado em Física

A aceleração da gravidade (g) é um tipo de aceleração, que é produzida pela atração gravitacional entre dois corpos.
Trata-se da aceleração de um corpo quando está em movimento de queda livre. Seu valor independe da massa dos corpos.
Lembre-se que a aceleração é uma grandeza vetorial que indica a variação da velocidade do movimento de um corpo ao longo do tempo.
Aceleração da Gravidade na Terra e na Lua
O campo gravitacional da Terra atrai todos os corpos para o centro do planeta. Sendo assim, a Terra exerce uma força sobre os corpos, a qual é chamada de força gravitacional.
A aceleração da gravidade nas proximidades da superfície da Terra é de 9,80665 m/s2 e esse valor normalmente é aproximado para 10 m/s2 para facilitar os cálculos.
Entretanto, seu valor não é constante. Isso porque o planeta não é uma esfera perfeita (os polos são achatados), e, portanto, a aceleração da gravidade varia em alguns pontos de sua superfície.
Como o valor da aceleração da gravidade depende da intensidade da força gravitacional, em lugares como a lua e outros planetas do sistema solar, a aceleração da gravidade é diferente do seu valor na Terra.
Por possuir massa menor que o nosso planeta, a aceleração da gravidade na lua é de 1,67 m/s2.
Fórmula
Segundo Newton e a Lei da Gravitação Universal, a aceleração da gravidade é o resultado da força de atração que a Terra exerce sobre todos os corpos.
Assim, o valor da aceleração da gravidade é calculada pela fórmula:
g = G . M/r²
Onde,
g: aceleração da gravidade
G: constante universal de gravitação
m: massa do planeta
r: distância do objeto ao centro do planeta
Força Peso
A força peso é a força resultante de atração dos corpos numa determinada interação gravitacional.
Note que o peso de um corpo varia conforme a força de gravidade exercida sobre ele. Assim, para calcular o peso dos corpos, utiliza-se a fórmula:
P = m . g
Onde:
P: peso
m: massa
g: aceleração da gravidade
Obs: o peso varia de acordo com a gravidade do local, já a massa de um corpo é sempre constante.
Força Gravitacional
Força Gravitacional ou interação gravitacional é a força que surge a partir da interação mútua entre dois corpos.
Atrativa e nunca repulsiva, é ela que torna possível ficarmos de pé. Isso porque a Terra exerce força gravitacional sobre os corpos.
Acontece entre a Terra e a Lua, bem como entre a Terra e o Sol, fazendo com que o movimento de translação da Terra aconteça.
Da mesma forma ocorre com todos os outros planetas. É a força gravitacional que os torna capazes de ficarem em suas órbitas girando ao redor do Sol.
Lei da Gravitação Universal
A Lei da Gravitação Universal foi proposta por Isaac Newton em 1666, na sequência do episódio clássico em que o cientista observa uma maçã cair da árvore.
Newton concluiu que a Terra e a maçã eram corpos que interagiam de forma recíproca.
Se não houvesse essa força, a Lua, por exemplo, cairia. Em virtude da gravidade, a Lua é atraída para o centro da Terra e sofre uma aceleração, a qual produz a sua órbita.
Além do movimento dos planetas, a Lei da Gravitação Universal também explica a altura das marés e o ciclo de vida das estrela. Importa lembrar que é a gravidade que mantém as estrelas vivas.
Fórmula
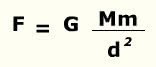
Onde,
F: força gravitacional entre dois corpos
G: Constante de gravitação universal
M e m: massa dos corpos (medida em quilogramas)
d: distância entre os centros dos corpos (medida em metros)
Isso quer dizer que a força é diretamente proporcional às massas e inversamente proporcional ao quadrado da distância entre os corpos.
A constante de gravitação universal é:
G = 6,67 x 10-8 dinas centímetro2/grama2
ou
G = 6,67 x 10-11 newtons metro2/quilograma2
De acordo com a Física, esse valor é o mesmo em qualquer local do universo.
Conclui-se que a Lei da Gravitação Universal obedece o princípio da proporcionalidade e que a sua interação é de longo alcance.
Energia potencial gravitacional é a energia que o corpo possui devido a atração gravitacional da Terra.
Desta forma, a energia potencial gravitacional depende da posição do corpo em relação a um nível de referência.
Fórmula
A energia potencial gravitacional é representada por Epg.
Pode ser calculada pelo trabalho que o peso deste corpo realiza sobre ele, quando cai de uma posição inicial até um ponto de referência.
Como o trabalho da força peso (Tp) é dado por:
Tp = m . g . h e Tp = Epg
Logo,
Epg = m . g . h
Sendo,
m o valor da massa do corpo. A unidade de medida da massa no sistema internacional (SI) é kg.
g o valor da aceleração da gravidade local. Sua unidade de medida no SI é m/s2.
h o valor da distância do corpo em relação a um nível de referência. Sua unidade no SI é m.
Usando as unidades acima, temos que a Epg é dada pela unidade kg.m/s2.m. Chamamos essa unidade de joule e usamos a letra J para representá-la.
Podemos concluir, através da fórmula, que quanto maior a massa de um corpo e a sua altura, maior será sua energia potencial gravitacional.
A energia potencial gravitacional, junto com a energia cinética e a energia potencial elástica compõem o que chamamos de energia mecânica.
Exemplo
Um vaso com uma flor está em uma varanda, no segundo andar de um prédio (ponto A). Sua altura em relação ao chão é de 6,0 m e sua massa é igual a 2,0 kg.
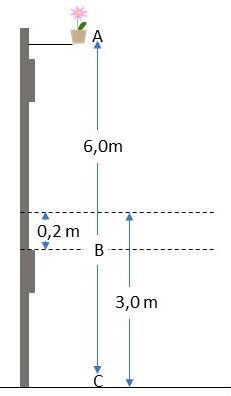
Considere a aceleração da gravidade local igual 10 m/s2. Responda:
a) Qual o valor da energia potencial gravitacional do vaso nesta posição?
Sendo,
m = 2,0 kg
ha = 6,0 m
g = 10 m/s2
Substituindo os valores, temos:
Epga = 2,0 . 6,0 . 10 = 120 J
b) O cabo que sustenta o vaso arrebenta e ele começa a cair. Qual o valor da sua energia potencial gravitacional, ao passar pela janela do primeiro andar (ponto B da figura)?
Primeiro calculamos a distância, em relação ao solo, do ponto B
h b = 3,0 – 0,2 = 2,8 m
Substituindo os valores, temos:
Epgb = 2,0 . 2,8 . 10 = 56 J
c) Qual o valor da energia potencial gravitacional do vaso, ao atingir o solo (ponto C)?
No ponto C a sua distância em relação ao solo é igual a zero.
Sendo assim:
Epgc = 2,0 . 0 . 10 = 0
Transformação da energia potencial gravitacional
Sabemos que a energia nunca pode ser destruída ou criada (princípio geral da conservação de energia). O que ocorre é que a energia está em constante transformação, se apresentando em diferentes formas.
As usinas hidrelétricas são um bom exemplo de transformação da energia.
A energia potencial gravitacional contida na água de uma represa elevada é convertida em energia cinética, movimentando as pás das turbinas da usina.
No gerador o movimento rotatório da turbina se converte em energia elétrica.

Usina Hidrelétrica, exemplo de transformação de energia.
As marés são movimentos oceânicos que ocorrem periodicamente, caracterizadas pela subida e descida no nível de água. Esse fenômeno ocorre em virtude da atração gravitacional exercida pela Lua e pelo Sol sobre o mar. De acordo com a Lei da Gravitação Universal, a Força gravitacional exercida por um corpo de massa m1 sobre outro corpo de massa m2, que estão separados pela distância d, é dada por:
Fg = G m1.m2
d2
Sendo que G é a constante de gravitação universal.
De acordo com essa equação, vemos que quanto maiores as massas e menores as distâncias, maior será a força gravitacional. Embora o Sol tenha massa muito maior que a Lua, a força gravitacional da Lua sobrepõe-se à do Sol porque a distância entre a Lua e a Terra é muito menor. Observe a figura abaixo:
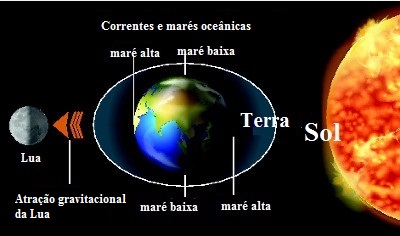
As marés ocorrem nas regiões próximas ao Sol ou à Lua
A imagem mostra como está atuando a força gravitacional sobre a água. As marés altas ocorrem nas regiões que estão mais próximas ao Sol e à Lua, enquanto nas demais regiões ocorrem as marés baixas.
Quando a água do mar está mais próxima da Lua, aquela é atraída por esta com uma força de maior intensidade do que nos demais pontos. Enquanto isso, na parte oposta da Terra, a água tende a afastar-se. Consequentemente, nos pontos intermediários, o nível do mar abaixa e ocorre a maré baixa.
Cada uma das marés acontece duas vezes em todos os pontos do planeta. Quando há o alinhamento entre o Sol, a Terra e a Lua, as forças gravitacionais sobrepõem-se e as marés ficam bem mais elevadas.

A existência das marés alta e baixa ocorre graças à atração gravitacional do Sol e da Lua
Fg = G . M . m
r2
Fg = 6,67 . 10-11 . 500 . 500
52
Fg = 6,67 . 10-7 N
3) Certo planeta A, que orbita em torno do Sol, tem período orbital de 1 ano. Se um planeta B, tem raio orbital 3 vezes maior, qual será o tempo necessário para que esse planeta complete uma volta em torno do Sol.
Resolução:
Para resolvermos o exercício, usaremos a Terceira Lei de Kepler, para tanto, basta identificar que o raio orbital do planeta B é igual a 3Ra, fazendo isso, temos que fazer o seguinte cálculo:
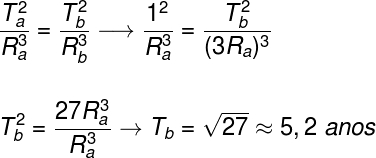
Agora faça os exercícios.
Exercícios.
O texto refere-se as questões 1 e 2.
Um tijolo de massa 250 g é lançado verticalmente para cima com velocidade de 10m/s. Desprezando a resistência do ar e adotando a aceleração da gravidade igual a 10 m/s², responda:
1) Qual a altura atingida pelo tijolo?
a) 2 m
b) 3 m
c) 4 m
d) 5 m
e) 6 m
2) Quanto tempo o tijolo leva para retornar ao ponto de lançamento?
a) 0.5 s
b) 1 s
c) 1,25 s
d) 1,5 s
e) 2 s
3) A força gravitacional é uma força que atua sobre dois corpos quaisquer e depende de suas massas e da distância entre eles. Entre a Terra e a Lua existe, portanto, uma força gravitacional. Se a distância da Lua à Terra caísse à metade, a força gravitacional seria:
a) quatro vezes maior.
b) duas vezes maior.
c) quatro vezes menor.
d) duas vezes menor.
e) igual.
4) A Terceira Lei de Kepler preconiza que os quadrados dos períodos de revolução dos planetas em torno do Sol é proporcional aos cubos dos seus respectivos raios médios de órbitas. De acordo com essa lei, podemos afirmar que:
a) quanto maior a distância do planeta ao Sol, maior a sua velocidade.
b) o Sol encontra-se no centro da órbita elíptica descrita pelos planetas.
c) quanto maior a distância do planeta ao Sol, menor a sua velocidade.
d) quanto maior for a massa de um planeta, menor é o seu período de revolução.
e) quanto menor for a massa de um planeta, menor é o seu período de revolução.
5) O fenômeno das marés é explicado pela Lei da Gravitação Universal, de Isaac Newton. A maré de sizígia, ou maré alta, ocorre quando as águas dos oceanos estão mais elevadas. Podemos afirmar que a maré de sizígia ocorre quando.
a) a Lua está mais afastada da Terra.
b) o Sol e a Lua estão perpendiculares em relação a Terra.
c) o Sol está mais afastado da Terra.
d) o Sol está mais próximo da terra.
e) o Sol e a Lua estão alinhados com a Terra
Nenhum comentário:
Postar um comentário
Não esqueça de colocar seu nome completo e série/ano turma