Resolver a sequência de atividades 5, pág. 83 a 86, caderno Aprender Sempre - Vol. único - 3ª série e enviar as imagens para meu e-mail institucional: silvanoprates@prof.educacao.sp.gov.br
até: 03/11.
Assistam as videoaulas:
quarta-feira, 28 de outubro de 2020
4° Bimestre - Atividade 2 - Recuperação - Habilidades em Defasagem
Obs.: Não precisa copiar a atividade da Apostila, somente responder no caderno e enviar as imagens das respostas via e-mail jociener@prof.educacao.sp.gov.br ou anexar no Google sala de aula. até 04/11/2020.
Assistir à aula relacionada nos links a seguir para e resolver os exercícios propostos.
ATV 3 - 4º BIM - CADERNO APRENDER SEMPRE - AULAS 5, 6 E 7 - PÁGINAS 14 A 18.
Assistir as videoaulas e responder os exercícios no Caderno do Aluno Aprender Sempre. Caso não tenha fiz o print das questões. Enviar as imagens das Atividades Respondidas para o e - mail:
silvanoprates@prof.educacao.sp.gov.br
ATÉ 03/11/2020.
Quando for enviar o e-mail, no campo assunto escreva: nome, série e número da atividade.
CADERNO APRENDER SEMPRE: AULAS 5, 6 E 7. PÁGINAS 14 A 18
Seguem algumas videoaulas:
FRAÇÕES: CONCEITOS E OPERAÇÕES - AULA 7: FRAÇÕES MISTAS OU NÚMEROS MISTOS
FRAÇÕES: CONCEITOS E OPERAÇÕES - FRAÇÕES NA RETA NUMERADA - AULA 8
MÚLTIPLOS E DIVISORES: DECOMPOSIÇÃO EM FATORES PRIMOS (AULA 8/12)
28/10 - 2ª série EM - Matemática - Os números irracionais
2A e 2B - Tudo bem com vocês? Favor copiar e resolver as questões abaixo, e enviar para o meu e-mail:helenabarcelos@prof.educacao.sp.gov.br, até o dia 12/11/2020.
1) Qual
alternativa representa a fração 9/2 em números decimais?
(a) 3,333 (b) 4,25 (c) 5,01 (d) 4,5
2) Qual
alternativa representa a fração 35/1000 em números decimais?
(a) 0,35
(b) 3,5 (c) 0,035 (d) 35
3) Qual
é a alternativa que representa o número 0,65 na forma de fração?
(a) 65/10 (b) 65/100 (c) 65/1000 (d) 65/10000
4) Observe as frações e suas respectivas
representações decimais.
I- 3/ 1000 = 0, 003 II- 2367/100 = 23, 67
III- 129/1000 = 0, 129 IV- 1,35/10 =
13,5
Utilizando
as igualdades acima, escolha a alternativa correta?
(a) I e II (b) I e IV (c) I, II e III (d) I,
II, III e IV
5) (VUNESP). A figura a seguir representa um
trecho da reta numérica em que estão destacados os números racionais 0, x, y e
1.
Analise as quatro afirmações seguintes a
respeito desses números
I. x . y < x II. 1/y > 1/x III. y/x > 1 IV. x/y < x
As únicas duas afirmações corretas são:
(a) I e II. ( b) I e III.
(c) I e IV. (d) II e III. ( e) II e IV.
6) O número decimal 0,03 pode ser
escrito por extenso como:
(a) três décimos
(b) três centésimos (c) três
milésimos (d) três milionésimo
7) Qual
é a diferença entre os números decimais 724,96 e 242,12?
(a)
48,284 (b) 586,28 (c) 241,59 (d) 482,00
8)Qual
alternativa representa a dízima periódica 0,555...
(a) 5/3 (b) 5/2 (c) 5/4 (d) 5/9
9) Associar as frações 3/2 , 9/2 e 1/2 com as
letras, de acordo com as suas posições na reta numérica.
(a) A =
1/2 ,B = 9/2 ,C = 3/2 (b) A = 9/2 ,B
= 3/2 ,C = 1/2 (c) A = 3/2 ,B = 1/2 ,C
= 9/2
(d) A=
7/2 , B= 9/6, C = 9/3
10) Qual
é a dízima periódica representada pela fração 10/3?
(a) 0,333... (b) 1,111... (c) 3,0303... (d)
3,333...
Programa de Recuperação- SA1
CADERNO DO ALUNO APRENDER SEMPRE
1° sério do ENSINO Médio - VOLUME 3
PROGRAMA DE RECUPERAÇÃO
SA1
Assistam às aulas do Centro de mídias, segue os links
https://m.youtube.com/watch?v=jp01mmjAb8I&list=PL1EAsbCb8zET9NLyK1Nu68Z84ywqwDiiR&index=47
https://m.youtube.com/watch?v=0hlAHc6uJS8&list=PL1EAsbCb8zET9NLyK1Nu68Z84ywqwDiiR&index=48
Aulas 5 e 6
A Relação da Equação com a Geometria
Atividade 1 item a e b página 16
Atividades 2 e 3 página 17
Item a, b, c, d e página 18
Atividade 4 página 18
Atividade 5 item a, b, c, d, e página 19
Atividade 6 item a, b, c, d, e página 20
do 1°Grau - EQUILIBRANDO A BALANÇA.
AULA 1 - PÁGINAS; 3 à 7
Atividades ; 01, 02, 03, 04 e 05
Realize os exercícios, fazendo todos cálculos não colocando apenas o resultados e envie para e-mail:
mariaaparecidamagalhaes@prof.sp.gov.br
Data prevista para entrega é dia 03/11 /2020.
Correção do roteiro de estudo: Soluções
Boa noite!
Vamos
corrigir o nosso roteiro de estudo e resolver exercícios de transformações
químicas no caderno.
Bom
estudo!!
1) O que
são soluções? Cite exemplos.
Soluções
são misturas homogêneas e podem ser encontradas nos estados de agregação gasoso,
líquido e sólido.
Exemplos:
álcool comum em solução aquosa, sal dissolvido em água, leite, sangue etc.
2) O que
é coeficiente de solubilidade?
A
medida da capacidade que um soluto possui de se dissolver em uma quantidade
padrão de solvente, em determinadas condições de temperatura e pressão.
3) O que
é concentração o em massa? Escreva a sua fórmula e o nome de cada grandeza
física.
A
concentração em massa (C) é a quantidade em massa de soluto (m1) que
se encontra dissolvidas em um volume padrão de solução (V) e normalmente é
expressa em g/L.
C = m1/V
C=
concentração
m1
= massa do soluto
V=
volume da solução
4) Intérprete a seguinte informação:
NaCl
(aq)
C = 12
g/L
a) Qual é
o soluto?
Cloreto
de sódio
b) Qual é
o solvente?
água
c) Quanto
há de soluto em cada litro de solução?
12
gramas para cada litro de solução
d) Quantos
mg de soluto há em cada mL de solução?
12.000
miligramas para cada mililitro de solução.
5) O que
é concentração mol/L (concentração em quantidade de matéria)? Escreva a sua fórmula
e o nome de cada grandeza física.
A
concentração em quantidade de matéria (M) ou concentração em mol/L é a relação entre a
quantidade de matéria (n1) e o volume da solução em litros (V).
M = n1/V
6) Interprete
a seguinte informação:
H2SO4
(aq)
M = 9,0
mol/L
a) Qual é
o solvente e o soluto?
Soluto:
ácido sulfúrico; solvente: água
b) Quantos
mols de soluto há por litro de solução?
9 mols
para cada litro de solução.
c) Quantos
gramas de soluto há por litro de solução?
882
gramas de soluto por litro de solução.
n1
= m1/MM
9,0 =
m1/98
m1=
9 . 98 = 882 gramas
98 é a
soma das massas atômicas do H2SO4
H2
= 2 . 1 = 2
S = 32
O = 4
. 16 = 64
2 = 32
= 64 = 98
d) Como
pode ter sido preparada essa solução?
Essa
solução foi preparada dissolvendo 9 mols de ácido sulfúrico em um litro de
solução.
Exercícios
1) Calcule
a concentração g/L de uma solução 300g de KOH em 950 mL de solução.
2) Qual é
a concentração em mol/L de uma solução aquosa preparada a partir de 23,4 g de
KCl, formando 2 L de solução?
3) Determine
a concentração em mol/L de uma solução de permanganato de potássio 0,395 g em
250 mL de solução.
Orientações:
·
Fazer a correção do roteiro de estudo.
·
Resolver os exercícios no caderno.
·
Dúvidas : elizangelamoura@prof,educacao.sp.gov.br
Termologia: revisão.
Recomendações aos alunos.
* Leiam o texto com atenção.* Assistam às aulas pelo CMSP, TV, vídeo aulas pela plataforma Stoodi.
* Façam pesquisas em livros didáticos ou pela internet.
* Identifiquem as atividades com o nome, série e n° de chamada ( se possível ), título da atividade e data de postagem no Blog.
* As atividades deverão ser enviadas para o e-mail: josecorreia@prof.educacao.sp.gov.br
* Identifiquem as atividades com o nome, série e n° de chamada ( se possível ), título da atividade e data de postagem no Blog.
* As atividades deverão ser enviadas para o e-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 03/11.
Olá pessoal! Que todos estejam bem.
Olá pessoal! Que todos estejam bem.
Nessa semana vamos revisar o estudo de termologia (estudo da temperatura). Para isso vamos começar com os conceitos de temperatura, calor e equilíbrio térmico.
- TEMPERATURA: é a medida da energia cinética das moléculas de uma substância.
Quanto maior for a agitação das moléculas, maior será a temperatura da substância. E quanto menor a agitação molecular, menor a temperatura.
A temperatura é medida por termômetros, que podem ser graduados nas escalas Celsius (°C), Fahrenheit (°F) ou Kelvin (K)
- CALOR: é a energia térmica em trânsito entre corpos ou sistemas, devido a diferença de temperatura entre eles.
O fluxo de energia térmica passa do corpo de maior temperatura para o de menor temperatura.
Como calor é uma forma de energia, sua unidade de medida, segundo o S.I., é o joule (J), porém é muito comum o uso da caloria (cal) como unidade de medida de calor.
- EQUILÍBRIO TÉRMICO: ocorre quando corpos com temperaturas diferentes trocam calor entre si, até atingirem o equilíbrio térmico.
- ESCALAS TERMOMÉTRICAS.
As escalas termométricas são usadas para indicar a temperatura, ou seja, a energia cinética associada à movimentação das moléculas.
No Sistema Internacional de Unidades (SI) a temperatura pode ser medida em três escalas:
- Escala Celsius (°C)
- Escala Kelvin (K)
- Escala Fahrenheit (°F)
Como referência, elas utilizam os pontos de fusão (gelo) e ebulição (vapor) da água. Confira abaixo a origem e as características de cada uma delas. Lembre-se que o termômetro é o instrumento utilizado para medir a temperatura.
Escala Fahrenheit
A Escala Fahrenheit foi criada em 1724 pelo físico e engenheiro Daniel Gabriel Fahrenheit (1686-1736). Recebe esse nome em homenagem ao seu criador.
Nos Estados Unidos e na Inglaterra a temperatura é medida em Fahrenheit. O símbolo dessa escala termométrica é °F.
- Ponto de Fusão da Água: 32 °C
- Ponto de Ebulição da Água: 212 °C
Escala Celsius
A Escala Celsius foi criada em 1742 pelo astrônomo sueco Anders Celsius (1701-1744). Recebe esse nome em homenagem ao seu criador.
É a escala termométrica mais utilizada no mundo, inclusive no Brasil. O símbolo dessa escala é °C.
- Ponto de Fusão da Água: 0 °C
- Ponto de Ebulição da Água: 100 °C
Obs: As expressões "Graus Celsius" e "Graus Centígrados" são sinônimas. No entanto, graus centígrados foi substituída pelo grau Celsius na Conferência Geral de Pesos e Medidas (1948).
Escala Kelvin
A Escala Kelvin é chamada de "escala absoluta" pois tem como ponto de referência o zero absoluto. Ela foi criada em 1864 pelo físico, matemático e engenheiro irlandês William Thomson (1824-1907). Recebe esse nome uma vez que ele também ficou conhecido como Lord Kelvin. O símbolo dessa escala termométrica é K.
- Ponto de Fusão da Água: 273 K
- Ponto de Ebulição da Água: 373 K
Fórmulas
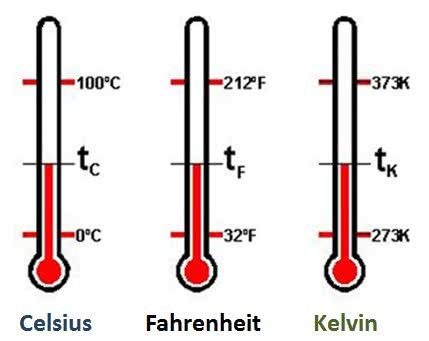
A fórmula utilizada para a conversão das escalas termométricas é:
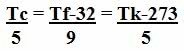
Donde,
- Tc: temperatura em Celsius
- Tf: temperatura em Fahrenheit
- Tk: temperatura Kelvin
De acordo com os pontos de fusão e ebulição de cada escala, podemos fazer a conversão entre elas:
Converter Celsius em Fahrenheit ou vice-versa:
Converter Celsius em Kelvin:
Converter Kelvin em Celsius:
Converter Kelvin em Fahrenheit ou vice-versa:
Exemplo
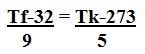
1) Para encontrar os valores equivalentes das escalas termométricas, basta adicionar o valor conhecido na fórmula, por exemplo:
Calcule o valor de 40 °C nas escalas Kelvin e Fahrenheit:
Celsius para Fahrenheit:
40/5 = tf -32/9
8 . 9 = Tf-32
72 = Tf – 32
72 + 32 = Tf
Tf = 104 °F
Celsius para Kelvin:
Tk = 40 + 273
Tk = 313 k
2) Converta 113°F para °C.
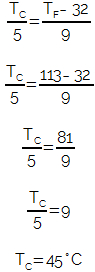
Quando um termômetro graduado na escala Fahrenheit marcar 113°F, um termômetro graduado em Celsius marcará 45°C. Essas duas temperaturas representam o mesmo estado de agitação molecular, só estão escritas em escalas termométricas diferentes.
A escala Celsius é a mais utilizada na maior parte dos países
3) Para medir a febre de pacientes, um estudante de medicina criou sua própria escala linear de temperaturas. Nessa nova escala, os valores de O (zero) e 10 (dez) correspondem, respectivamente, a 37°C e 40°C. A temperatura de mesmo valor numérico em ambas as escalas é aproximadamente:
Resolução:
Comparando as escalas, temos:
ϴC - 37 = ƟX – 0
40 -37 10 – 0
ϴC - 37 = ƟX
3 10
Se Ɵ é a temperatura de mesmo valor numérico em ambas as escalas, então podemos dizer que ƟX – Ɵc = Ɵ. Logo, temos:
ϴ- 37 = Ɵ_
3 10
10Ɵ – 370 = 3ϴ
7Ɵ = 370
Ɵ = 370/7
Ɵ = 52,9 °C ou 52,9°X
4) Uma panela com água é aquecida de 25°C para 80°C. A variação de temperatura sofrida pela panela com água, nas escalas Kelvin e Fahrenheit, foi de:
a) 32 K e 105°F.
b) 55 K e 99°F.
c) 57 K e 105°F.
d) 99 K e 105°F.
e) 105 K e 32°F.
Resolução:
Primeiro precisamos saber qual foi a variação na escala Celsius. Esse valor é obtido através da diferença entre o valor final e o valor inicial:
ΔC = C2 - C1
ΔC = 80-25
ΔC = 55 °C
Quando a temperatura varia 1° na escala Celsius, ela sofre a mesma variação na escala Kelvin. Portanto, se a variação foi de 55° na escala Celsius, também foi de 55 em na escala Kelvin.
Na escala Fahrenheit, essa mesma variação é dada por:
C = F
5 9
Substituindo C por 55, temos:
55 = F
5 9
11 = F
9
F = 9.11
F = 99 °F
De acordo com os resultados obtidos, a alternativa correta é a letra b.
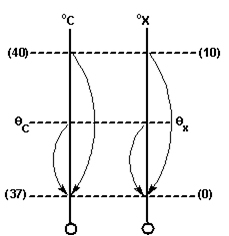
5) Um estudante de física criou uma escala (°X), comparada com a escala Celsius ele obteve o seguinte gráfico:
a. Qual a equação de conversão entre as duas escalas?
b. Qual a temperatura do corpo humano (37°C) nesta escala?
a) 
b)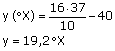 
Assistam a vídeo aula com o Professor Marcelo Boaro através do Link:
https://youtu.be/6H5OOCTdPeo
Vídeo disponível no YouTube.
Agora façam os exercícios que seguem.
EXERCÍCIOS.
1) Teoricamente, na temperatura do zero absoluto (-273,15°C), o que seria nulo?
a) A quantidade de partículas de um gás.
b) O volume de um corpo.
c) A agitação térmica das moléculas da substância.
d) A altura da coluna de mercúrio.
e) A pressão do gás.
2) Ao comprar um termômetro em um país estrangeiro, um estudante de Física percebeu que a temperatura medida era de 77 ºF. Qual seria o valor dessa temperatura na escala absoluta?
a) 313 K
b) 298 K
c) 285 K
d) 273 K
e) 290 K
3) A escala Reamur de temperatura, que hoje está em desuso, adotava para o ponto de gelo 0°R e para o ponto de vapor 80°R. A indicação que, nessa escala, corresponde a 30°C é:
a) 24°R
b) 20°R
c) 14°R
d) 36°R
e) 48°R
4) Alguns corpos apresentam características físicas que variam com a temperatura, as quais são chamadas de propriedades termométricas. Os termômetros se utilizam dessas propriedades para medir temperatura. Analise as proposições I, II e III abaixo.
I. A pressão de um gás a volume constante é considerada uma propriedade termométrica.
II. A resistência elétrica é considerada uma propriedade termométrica.
III. A massa de um corpo é considerada uma propriedade termométrica.
a) Apenas a proposição I está correta.
b) As proposições I, II e III estão corretas.
c) Apenas as proposições I e III estão corretas.
d) Apenas a proposição II está correta.
e) Apenas a proposição I e II estão corretas.
5) O gráfico abaixo indica a relação de temperatura entre dois termômetros, um graduado na escala Celsius (°C) e outro graduado numa escala arbitrária (°X).
Ao medir a temperatura de um líquido, o termômetro registrou 35°X. Qual é a temperatura correspondente na escala Celsius?
a) 40°C
b) 35°C
c) 30°C
d) 25°C
e) 20°C
Assinar:
Postagens (Atom)