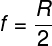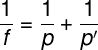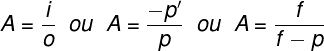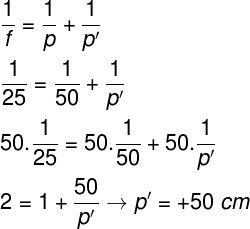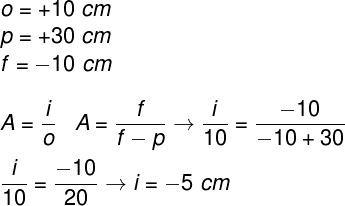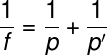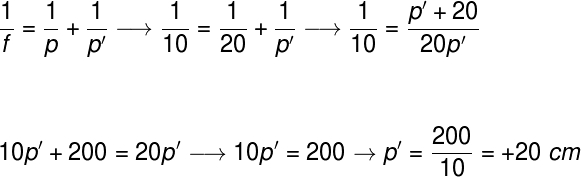Recomendações aos alunos:
* Leiam com atenção e observem os exemplos.
* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.
* Façam pesquisas em livros didáticos ou pela internet.
* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 29/09.
Olá pessoal! Que todos estejam bem.
Nessa semana vamos continuar o nisso estudo de óptica geométrica. Vamos estudar as imagens formadas em espelhos esféricos.
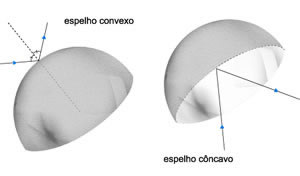
Os espelhos esféricos podem ser côncavos ou convexos.
É muito importante que se identifique três pontos de um espelho esférico, o centro de curvatura, a distância focal e o vértice do espelho. Além do eixo óptico, ou eixo principal do espelho.
Dependendo da posição do objeto em relação a esses pontos, a imagem será modificada, podendo ficar maior, menor, real, virtual, direita ou invertida.
Chamamos espelho esférico qualquer calota esférica que seja polida e possua alto poder de reflexão.

É fácil observar-se que a esfera da qual a calota acima faz parte tem duas faces, uma interna e outra externa. Quando a superfície refletiva considerada for a interna, o espelho é chamado côncavo. Já nos casos onde a face refletiva é a externa, o espelho é chamado convexo.
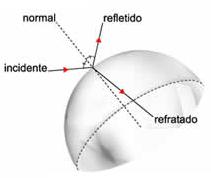
Reflexão da luz em espelhos esféricos
Assim como para espelhos planos, as duas leis da reflexão também são obedecidas nos espelhos esféricos, ou seja, os ângulos de incidência e reflexão são iguais, e os raios incididos, refletidos e a reta normal ao ponto incidido.
Aspectos geométricos dos espelhos esféricos
Para o estudo dos espelhos esféricos é útil o conhecimento dos elementos que os compõe, esquematizados na figura abaixo:
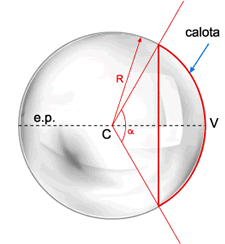
C é o centro da esfera;
V é o vértice da calota;
O eixo que passa pelo centro e pelo vértice da calota é chamado eixo principal.
As demais retas que cruzam o centro da esfera são chamadas eixos secundários.
O ângulo
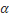
, que mede a distância angular entre os dois eixos secundários que cruzam os dois pontos mais externos da calota, é a
abertura do espelho.
O raio da esfera R que origina a calota é chamado raios de curvatura do espelho.
Um sistema óptico que consegue conjugar a um ponto objeto, um único ponto como imagem é dito estigmático. Os espelhos esféricos normalmente não são estigmáticos, nem aplanéticos ou ortoscópicos, como os espelhos planos.
No entanto, espelhos esféricos só são estigmáticos para os raios que incidem próximos do seu vértice V e com uma pequena inclinação em relação ao eixo principal. Um espelho com essas propriedades é conhecido como espelho de Gauss.
Um espelho que não satisfaz as condições de Gauss (incidência próxima do vértice e pequena inclinação em relação ao eixo principal) é dito astigmático. Um espelho astigmático conjuga a um ponto uma imagem parecendo uma mancha.
Focos dos espelhos esféricos
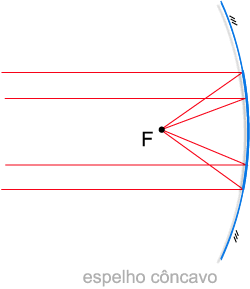
Para os espelhos côncavos de Gauss, pode-se verificar que todos os raios luminosos que incidirem ao longo de uma direção paralela ao eixo secundário passam por (ou convergem para) um mesmo ponto F - o foco principal do espelho.
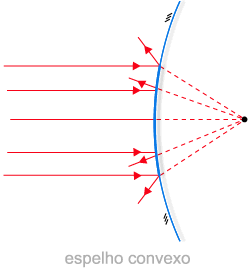
No caso dos espelhos convexos, a continuação do raio refletido é que passa pelo foco. Tudo se passa como se os raios refletidos se originassem do foco.
Características das imagens nos espelhos esféricos
As características das imagens nos espelhos esféricos mudam de acordo com quando mudamos a posição do objeto na frente do espelho.
Temos dois tipos de imagem, virtual e real:
- Imagem virtual: é vista no ponto de encontro dos prolongamentos dos raios refletidos
- Imagem real: é vista em um ponto onde realmente passam os raios refletidos
Podemos dizer como as imagens irão se comportar sabendo qual a posição do objeto em relação ao espelho:
Espelhos Côncavos
- Objeto localizado antes do centro de curvatura (C): A imagem é real, está posicionada entre o centro de curvatura(C) e o foco(F), é invertida e o seu tamanho é menor que o objeto.
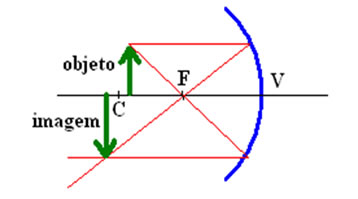
- Objeto localizado sobre o centro de curvatura (C): A imagem é real, está posicionada sobre o centro de curvatura(C), é invertida e tem o mesmo do objeto.
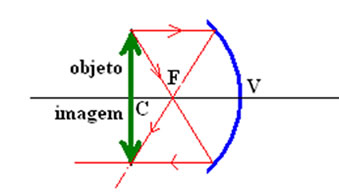
- Objeto localizado entre o centro de curvatura (C) e o foco (F): A imagem é real, está posicionada antes do centro de curvatura(C), é invertida e o seu tamanho é maior que o objeto.
- Objeto localizado sobre o foco (F): A imagem é imprópria, pois os raios de luz saem paralelos.
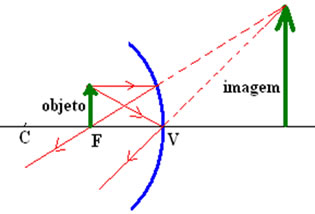
- Objeto localizado entre o foco (F) e o vértice (V): A imagem é virtual, está posicionada atrás do espelho ou depois do vértice(V), é direita e o seu tamanho é maior que o objeto.
Os espelhos côncavos são muito usados por mulheres para passar maquiagem no rosto, pois amplia a imagem.
Espelhos Convexos
A imagem nos espelhos convexos sempre será virtual, estará posicionada entre o foco(F) e o vértice(V), será direita e o seu tamanho será menor que o objeto.
Os espelhos convexos são bastante utilizados nos retrovisores direito dos carros, pois diminui a imagem para que caibam mais imagens no espelho, dando assim uma ampla visão.
Construção de imagens
Espelho convexo
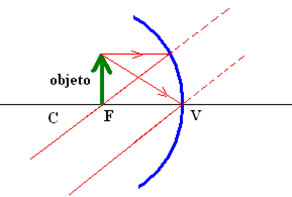
Caso um objeto qualquer seja colocado diante de um espelho convexo, usaremos dois raios para construir a imagem. Como mostra a figura, a imagem do objeto estará no encontro dos prolongamentos dos raios refletidos.
Espelho côncavo
1 – Objeto real antes do centro de curvatura:
A imagem formada é real, invertida e menor que o objeto.
2 – Objeto real no centro de curvatura:
A imagem formada é real, invertida e do mesmo tamanho do objeto.
3 – Objeto real entre o centro de curvatura e o foco:
A imagem formada é real, invertida e maior que o objeto.
4 – Objeto real no foco:
A imagem é imprópria, ou seja, localizada no infinito.
5 – Objeto real entre o foco e o vértice:
A imagem é virtual (atrás do espelho), direita e maior que o objeto.

Espelho esférico do tipo convexo
Publicado por: Domiciano Correa Marques da Silva
Fórmulas sobre espelhos esféricos
As fórmulas utilizadas para o estudo analítico de espelhos esféricos valem tanto para os espelhos côncavos como para os espelhos convexos. A principal diferença entre esse tipo de espelhos é o sinal algébrico que é atribuído ao foco (f).
Espelhos convexos, que apresentam foco virtual, apresentam foco negativo, enquanto os espelhos côncavos, cujos focos são reais, apresentam foco positivo. Além disso, é importante que se defina um referencial para a utilização de sinais algébricos, para tanto, utiliza-se o referencial de Gauss. De acordo com o referencial de Gauss:
Qualquer objeto ou imagem que se encontra à frente da superfície refletora do espelho deverá receber sinal positivo.
Qualquer objeto ou imagem que se encontra atrás da superfície refletora do espelho deverá receber sinal negativo.
Qualquer objeto ou imagem que tenha orientação vertical para cima deverá receber sinal positivo.
Qualquer objeto ou imagem que tenha orientação vertical para baixo deverá receber sinal negativo.
A figura a seguir traz um pequeno esquema para facilitar o entendimento dos sinais utilizados segundo o referencial de Gauss:
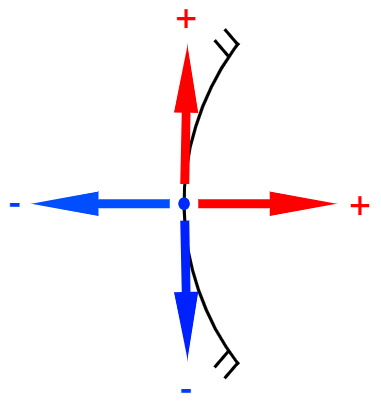
Denotamos pela letra p a posição dos objetos em relação ao vértice dos espelhos. A posição das imagens conjugadas pelos espelhos, por sua vez, é denotada pela letra p'. Em posse dessas afirmações, vamos às fórmulas.
Distância focal e raio de curvatura
Há uma fórmula válida para todos os espelhos esféricos que relaciona a distância focal ao raio de curvatura, confira:
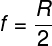
f - distância focal
R - raio de curvatura
Equação dos pontos conjugados ou Equação de Gauss
A equação dos pontos conjugados relaciona a distância focal (f), a posição do objeto (p) e a posição da imagem (p'), ambas medidas em relação ao vértice do espelho, confira:
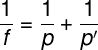
f - distância focal
p - posição do objeto
p' - posição da imagem
Equação do aumento linear transversal
Aumento linear transversal é a grandeza adimensional (sem unidade de medida) que mede a relação entre o tamanho do objeto e o de sua imagem conjugada por espelhos esféricos. Existem três formas diferentes de calcularmos o aumento linear transversal, confira:
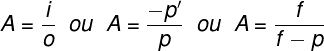
A - aumento linear transversal
i - tamanho da imagem
o - tamanho do objeto
f - distância focal
Para entender melhor o significado do aumento linear transversal, confira alguns resultados possíveis e suas interpretações:
A = 1: nesse caso, a imagem tem o mesmo tamanho do objeto e sua orientação é positiva (imagem virtual);
A = -1: nesse caso, a imagem tem o mesmo tamanho do objeto, no entanto, é invertida (imagem real);
A = + 0,5: imagem virtual (direita) com metade do tamanho do objeto;
A = - 2,5: imagem real (invertida) com 2,5 vezes o tamanho do objeto.
Exemplos.
1) Um objeto é posicionado 50 cm à frente de um espelho côncavo, cuja distância focal é de 25 cm. Determine em qual posição forma-se a imagem desse objeto.
Resolução:
Para resolvermos esse exercício, será necessária a equação de Gauss, observe os cálculos:
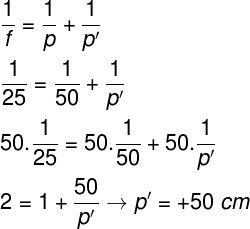
2) Um objeto de 10 cm de altura é colocado a 30 cm de um espelho convexo, cuja distância focal é -10 cm. Determine o tamanho da imagem conjugada por esse espelho.
Resolução:
Para resolvermos esse exercício, faremos uso da equação do aumento linear transversal, confira o cálculo a ser feito:
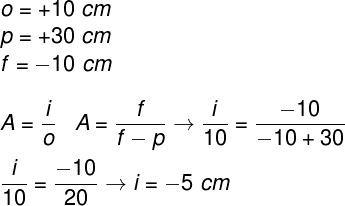
Isso indica que a imagem é reduzida em relação ao objeto e invertida, portanto, real.
3) Certo espelho côncavo tem raio de curvatura de 0,5 m. Qual é a distância focal desse espelho, em cm?
Resolução:
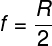
f = 0,5/2
f = 0,25 m (multiplica por 100 para passar de metros para centímetros)
f = 25 cm
4) Um espelho esférico conjuga uma imagem virtual, direta e reduzida de um objeto real. Em relação a esse espelho e à posição do objeto da imagem, assinale a alternativa correta:
a) Trata-se de um espelho côncavo, quando o objeto é posicionado entre seu foco e vértice.
b) Trata-se de um espelho côncavo, quando o objeto é posicionado no foco do espelho.
c) Trata-se de um espelho côncavo, quando o objeto é colocado no centro de curvatura do espelho.
d) Trata-se de um espelho convexo, quando o objeto é colocado a qualquer distância de seu vértice.
e) Trata-se de um espelho convexo que conjuga imagens reais.
Resolução:
O único espelho capaz de produzir imagens diretas e reduzidas é o espelho convexo, independentemente de qual seja a distância entre o objeto e o espelho. Por isso, a alternativa correta é a letra D.
5) Um espelho esférico côncavo conjuga uma imagem real de um objeto que é colocado a 20 cm de seu vértice. Sabendo que a distância focal desse espelho é de 10 cm, determine a distância dessa imagem formada até o objeto.
Resolução:
Para calcularmos a posição da imagem conjugada pelo espelho, utilizamos a equação dos pontos conjugados (equação de Gauss):
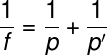
Utilizando os dados fornecidos pelo exercício, como o foco de 10 cm e a posição do objeto em relação ao espelho, de 20 cm, faremos o seguinte cálculo:
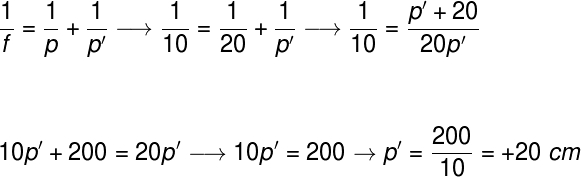
Para resolução desse cálculo, deve-se fazer o m.m.c. (20, P') = 20P', dividir pelo de baixo e multiplicar pelo de cima. Como a distância da imagem é a mesma do objeto, a distância entre o objeto e sua imagem é 0 cm. Pois 20 cm - 20 cm = 0.
Resposta: A distância entre o objeto e a imagem é 0 cm.
Observação:
Vocês podem assistir às vídeo aulas na plataforma Stoodi ou a vídeo aula do Professor Boaro, através do link: https://youtu.be/q3bgLFmW4Rs (vídeo disponível no YouTube)
Agora faça os exercícios.
Exercícios.
1) Motivado a enxergar mais carros que se aproximem da traseira do seu veículo, um motorista resolveu instalar um espelho esférico em um de seus retrovisores. Para sua surpresa, ele obteve somente imagens invertidas dos carros distantes. Qual foi o tipo de espelho escolhido pelo motorista e qual espelho seria a escolha correta?
a) plano e esférico, respectivamente
b) côncavo e convexo, respectivamente
c) convexo e côncavo, respectivamente
d) convexo e parabólico, respectivamente
e) esférico e plano, respectivamente
2) Um objeto é posicionado 40 cm à frente de um espelho côncavo, cuja distância focal é de 20 cm. Determine em qual posição forma-se a imagem desse objeto.
a) 20 cm
b) 30 cm
c) 40 cm
d) 50 cm
e) 60 cm
3) Um objeto de 15 cm de altura é colocado a 40 cm de um espelho convexo, cuja distância focal é -20 cm. Determine o tamanho da imagem conjugada por esse espelho.
a) 5 cm
b) 4 cm
c) 6 cm
d) 3 cm
e) 7 cm
4) Sabendo que um espelho côncavo tem 60 cm de raio de curvatura, e que segue as condições de Gauss. Podemos afirmar que a distância focal desse espelho é:
a) 60 cm
b) 50 cm
c) 40 cm
d) 30 cm
e) 20 cm
5 ) Um objeto está sobre o eixo de um espelho esférico côncavo. A distância entre o objeto e o espelho é maior que o raio de curvatura do espelho. A imagem do objeto é:
a) real, não invertida, menor que o objeto;
b) real, invertida, maior que o objeto;
c) virtual, invertida, menor que o objeto.
d) virtual, não invertida, maior que o objeto;
e) real, invertida, menor que o objeto.

.jpg)
(1).jpg)