* Leiam os textos com atenção e observem os exemplos.
* Assistam às aulas pelo CMSP, TV, plataforma Stoodi.
* Pesquisem em livros didáticos ou pela internet.
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 04/08.
Semana de estudos intensivos.
Olá pessoal! Vamos fazer a revisão do que aprendemos nesse 2° bimestre.
- Campo magnético: é a região do espaço, onde qualquer material ferromagnético sofre a ação de uma força magnética, originada por imãs ou por um objeto que foi imantado.
O campo magnético é representado por linhas de força do campo magnético. Veja:
Característica das linhas de força do campo magnético:
1) As linhas de força saem do polo norte e vão para o polo sul magnético.
2) As linhas de força nunca se cruzam.
3) Nas regiões em que as linhas de força estão mais próximas umas das outras, a intensidade do campo magnético é maior do que nas regiões onde as linhas estão mais afastadas umas das outras.
4) O vetor campo magnético é tangente à linha de força num ponto e tem o mesmo sentido da linha de força.
- Campo magnético terrestre.
O planeta Terra tem um campo magnético. A bússola funciona devido ao campo magnético do planeta. O polo norte magnético aponta na direção aproximada do norte geográfico do planeta. Isso prova que o polo norte geográfico corresponde ao polo sul magnético, e o polo sul geográfico ao polo norte magnético. Veja:
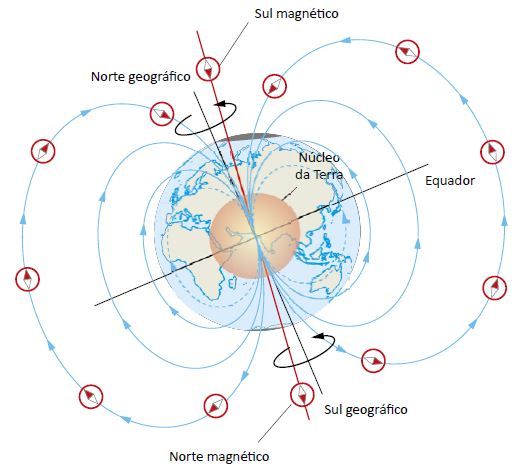
A hipótese mais aceita para o magnetismo do planeta, é que devido a alta temperatura no centro da Terra, há níquel no estado líquido em movimento. Como níquel é um metal ferromagnético, e todo metal possui elétrons livres, cargas elétricas em movimento criam campos magnéticos.
De acordo com o experimento de Oersted, cargas elétricas em movimento criam campo magnético e campo magnético em movimento geram corrente elétrica.
As Auroras Boreais e Austrais são formadas devidos aos ventos solares que incidem com o campo magnético do planeta.
Alguns animais, como pássaros, e algumas bactérias, como as bactérias magnéticas, se orientam pelo campo magnético da Terra.
- Campo magnético ao redor de um condutor retilíneo longo.
Um fio retilíneo, ao ser percorrido por uma corrente elétrica (i), cria um campo magnético ao seu redor. Observe a figura.
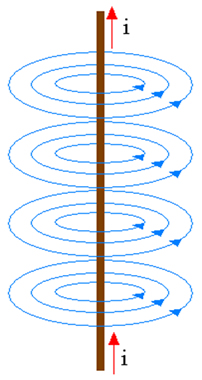
O campo magnético gerado por um fio retilíneo é calculado através da fórmula:
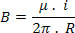
Onde:
B = campo magnético ( tesla(T))
μ = permeabilidade magnética do meio, no vácuo μ = 4π . 10-7 T.m/A.
i = corrente elétrica (ampère(A))
R = distância do fio até um ponto (metros(m))
No S.I., a unidade de medida de campo magnético é o tesla (T), em homenagem a Nicola Tesla.
- Regra da mão direita: é utilizada para determinar o sentido do campo magnético.
O polegar é colocado no mesmo sentido da corrente elétrica (i), e os demais dedos circulam em torno do fio indicando se o campo magnético entra ou sai do plano.
Na figura, o campo magnético sai do plano pelo lado esquerdo da figura e entra no plano pelo lado direito da figura.
.jpg)
. x
Para representar o sentido do campo magnético é utilizado os símbolos:
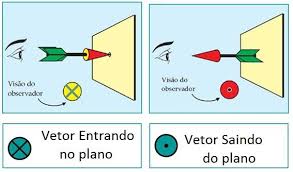
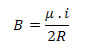
Através da regra da mão direita podemos ver que o vetor B está na vertical.
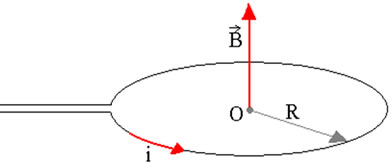
- Campo magnético gerado por uma espira.
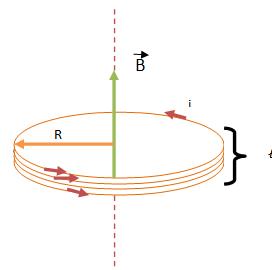
Considere que um fio condutor retilíneo seja percorrido por uma corrente elétrica contínua. Considere também que esse mesmo fio seja encurvado para formar uma espira plana circular de raio R, percorrida por uma corrente elétrica de intensidade i, conforme mostra a figura acima.
Em uma espira circular plana, as linhas do campo magnético são circunferências perpendiculares ao seu plano, concêntricas com o condutor. O vetor indução magnética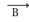
no centro O dessa espira tem as seguintes características:
Em uma espira circular plana, as linhas do campo magnético são circunferências perpendiculares ao seu plano, concêntricas com o condutor. O vetor indução magnética
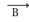no centro O dessa espira tem as seguintes características:
- intensidade: a intensidade do vetor .jpg)
no centro da espira é dada pela expressão:
no centro da espira é dada pela expressão:
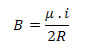
- direção: normal ao plano da espira;
- sentido: dado pela regra da mão direita.
- sentido: dado pela regra da mão direita.
Através da regra da mão direita podemos ver que o vetor B está na vertical.
Onde:
B = campo magnético (tesla(T))
μ = 4π . 10-7 T.m/A.
i = corrente elétrica (ampère(A))
R = raio da espira (metros(m))
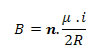
.jpg)
Campo Magnético no interior de um solenoide.
Solenoide
B = campo magnético (tesla(T))
μ = 4π . 10-7 T.m/A.
i = corrente elétrica (ampère(A))
R = raio da espira (metros(m))
- Campo magnético gerado por bobinas chatas.
Se considerarmos n espiras iguais justapostas, ou seja, uma do lado da outra, de modo que a espessura do enrolamento seja muito menor que o diâmetro de cada espira, teremos a chamada bobina chata. A intensidade do vetor indução magnética B no centro O da bobina chata é determinada através da seguinte equação:
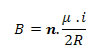
Onde:
B – é o campo magnético no interior da espira (ou bobina)
i – é a corrente elétrica
R – é o raio da espira (ou bobina)
μ – é a permeabilidade magnética
n – é o número de voltas da bobina
B – é o campo magnético no interior da espira (ou bobina)
i – é a corrente elétrica
R – é o raio da espira (ou bobina)
μ – é a permeabilidade magnética
n – é o número de voltas da bobina
- Campo magnético gerado por um solenoide.
Denomina-se solenoide um fio condutor, longo, enrolado, que forma uma bobina em espiral.
Ao ser percorrido pela corrente i, surge no interior do solenoide um campo magnético cujas linhas de indução são praticamente paralelas. O campo magnético no interior do solenoide é praticamente uniforme.
Nessas condições, em cada ponto do interior do solenoide, o vetor indução magnética tem as seguintes características:
• direção: é a do enxó do solenoide;
• sentido: é dado pela regra da mão direita;
• Intensidade: Sendo N o número de espiras existentes no comprimento l, a intensidade do vetor B é dada por:
.jpg)
Onde:
μ é a constante de permeabilidade magnética do meio;
N é o número de espiras do solenoide;
l é o comprimento do solenoide;
i é a intensidade de corrente elétrica.
Ao ser percorrido pela corrente i, surge no interior do solenoide um campo magnético cujas linhas de indução são praticamente paralelas. O campo magnético no interior do solenoide é praticamente uniforme.
Nessas condições, em cada ponto do interior do solenoide, o vetor indução magnética tem as seguintes características:
• direção: é a do enxó do solenoide;
• sentido: é dado pela regra da mão direita;
• Intensidade: Sendo N o número de espiras existentes no comprimento l, a intensidade do vetor B é dada por:
Onde:
μ é a constante de permeabilidade magnética do meio;
N é o número de espiras do solenoide;
l é o comprimento do solenoide;
i é a intensidade de corrente elétrica.
Campo Magnético no interior de um solenoide.
Da mesma forma que a espira, um solenoide apresenta dois polos. Portanto, de acordo com a regra da mão direita, as linhas de indução magnética são perpendiculares ao plano do centro das espiras.
Solenoide
- Força magnética sobre cargas elétricas.
Para calcular a intensidade da força magnética (seu módulo) sobre uma carga elétrica que está em movimento dentro de um campo magnético, podemos usar a seguinte fórmula:
F = ∣q∣ .v.B.sen(θ)
- F é a intensidade da força magnética, normalmente dada em Newtons (N);
- ∣ q∣ é o módulo da carga elétrica, ou seja, não levamos em conta seu sinal, normalmente dada em Coulomb (C);
- v é a velocidade da carga elétrica, normalmente dada em metros por segundo (m/s);
- B é o valor do campo magnético, normalmente dada em Tesla (T);
- sen(θ) é o seno do ângulo entre o vetor da velocidade com o vetor do campo magnético;
- Regra da mão esquerda: é utilizada para determinar o sentido da força magnética. Veja:
A regra da mão esquerda, chamada de “regra da mão esquerda de Fleming”, também é usada para encontrar o sentido da força magnética.
O dedo polegar representa o sentido da força magnética (F). Já o dedo indicador representa o campo magnético (B), ou seja, o sentido da corrente elétrica. O dedo médio indica o sentido da velocidade (v).
Para compreender melhor, veja a figura abaixo:
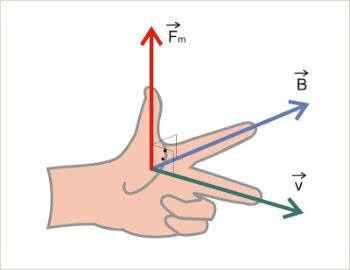
Observação: o sentido dessa força magnética é para uma carga positiva. No caso de uma carga negativa, a direção será a mesma, mas o sentido da força será contrário ao dado pela regra da mão esquerda (em vez de apontar para unha, apontará para dentro da mão).
- Força magnética sobre fio conduzindo corrente elétrica.
Ao colocarmos um determinado fio percorrido por uma corrente elétrica dentro de um campo magnético, verifica-se que ele sofre a ação de uma força, que chamamos de força magnética, representada pela letra F.
Em um condutor retilíneo percorrido por corrente elétrica de intensidade i, cada uma das cargas, que se movem com uma velocidade v, fica sujeita à ação de uma força magnética cuja intensidade é F e é dada pela equação:
F = B.i.l.senӨ
Onde:
F = força magnética (newton(N))
B = campo magnético (tesla(T))
i = corrente elétrica (ampère(A))
l = comprimento do fio (metros(m))
sen Θ = seno do ângulo formado entre a corrente elétrica (i) e o campo magnético (B)
Observações:
Se o ângulo formado entre a corrente e o campo é de 90°, temos que sen 90° = 1
Se o ângulo formado entre a corrente e o campo é de 0°, ou seja, paralelos, temos que sen 0° = 0, e portanto a força magnética será nula ( F = 0 ).
Exemplos.
1) Vamos supor que uma corrente elétrica de intensidade igual a 5 A esteja percorrendo um fio condutor retilíneo. Calcule a intensidade do vetor indução magnética em um ponto localizado a 2 cm do fio. Adote μ= 4π.10-7 T.m/A.
Resolução:
Sabemos que a intensidade do vetor indução magnética no ponto P, devido à corrente elétrica i, é dada pela seguinte relação:
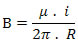
Retirando os dados fornecidos pelo exercício e substituindo-os na equação acima, temos:
i = 5 A, R = 2 cm = 0,02 = 2 . 10-2 m
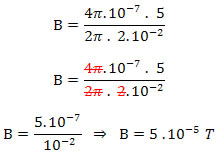
2) Uma espira circular de raio π é atravessada por uma corrente elétrica de 0,5A. Sendo a permeabilidade magnética do vácuo de μ = 4π . 10-7 T.m/A., determine a indução magnética no interior dessa espira.
Resolução:
R = π
i = 0,5A
μ = 4π . 10-7 T.m/A
B = ?
B = μ . i/2.R
B = 4π . 10-7 . 0,5/2.π
B = 2 . 10-7 /2
B = 10-7 T
3) Uma bobina chata é formada de 50 espiras circulares de raio 10 cm. Sabendo que as espiras são percorridas por uma corrente de 3 A, a intensidade do vetor campo magnético no seu centro será de:
Obs: considere µ0 = 4π . 10-7 T.m/A.
B = μ . i . n
2.R
B = 4π.10-⁷ . 3 . 50
2 . 0,1
B = 600π .10-⁷
0,2
B = 3000π . 10-⁷
B = 3π . 10-⁴ T
4) Considere um longo solenoide ideal composto por 10.000 espiras por metro, percorrido por uma corrente contínua de 0,2 A. O módulo e as linhas de campo magnético no interior do solenoide ideal são, respectivamente:
Resolução:
Considerando que o solenoide tenha apenas 1 m, o número de espiras a ser considerado é de 10.000 (104). Assim, o campo magnético para esse solenoide é:
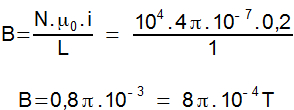
As linhas de campo magnético de um solenoide formam linhas paralelas ao eixo do solenoide, saindo do polo norte (N) e entrando no polo sul (S).
5) Um fio condutor retilíneo tem comprimento L = 16 metros e transporta uma corrente elétrica contínua, igual a I = 0,5 A, em um local onde existe um campo magnético perpendicular e uniforme, cujo módulo vale B = 0,25 Tesla, conforme indica a figura abaixo. O módulo da força magnética exercida pelo campo magnético sobre o fio será:
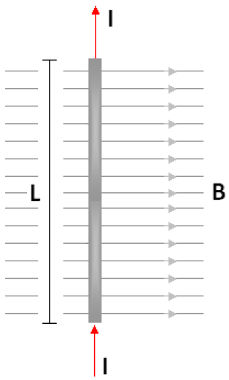
Resolução:
Aplicando a equação da força magnética sobre o fio retilíneo, teremos:
Agora faça você.
Exercícios.
1) A hipótese mais aceita pera se explicar o magnetismo da Terra é:
a) Devido ao movimento de níquel no estado líquido no centro do planeta.
b) Devido ao fato de que a agulha de uma bússola aponta para a direção Norte - Sul do planeta.
c) devido ao fato de existirem bactérias magnéticas no solo.
d) devido ao fato dos pássaros se orientarem de acordo com o polo Norte geográfico da Terra.
e) devido às auroras Boreais e Austrais.
2) A bússola representada na figura abaixo repousa sobre sua mesa de trabalho. O retângulo tracejado representa a posição em que você vai colocar um ímã, com os polos respectivos nas posições indicadas. Em presença do ímã, a agulha da bússola permanecerá como em:
.gif)
3) Vamos supor que uma corrente elétrica de intensidade igual a 2 A esteja percorrendo um fio condutor retilíneo. Calcule a intensidade do vetor indução magnética em um ponto localizado a 8 cm do fio. Adote μ= 4π.10-7 T.m/A.
a) 5 .10⁶ T
b) 5 .10³ T
c) 5 . 10-⁶ T
e) 5 . 10⁵ T
4) Uma espira circular de raio 2π é atravessada por uma corrente elétrica de 4 A. Sendo a permeabilidade magnética do vácuo de μ = 4π . 10-7 T.m/A., determine a indução magnética no interior dessa espira.
a) 4 . 10-² T
b) 4 . 10-³ T
c) 4 . 10-⁵T
d) 4 . 10-⁷ T
e) 4 . 10-⁶ T
5) Uma bobina chata é formada de 100 espiras circulares de raio 40 cm. Sabendo que as espiras são percorridas por uma corrente de 4 A, determine a intensidade do campo magnético gerado pela bobina.
a) 2π . 10² T
b) 2π . 10 ³ T
c) 2π . 10-² T
d) 2π . 10-⁶ T
e) 2π . 10-⁴ T
