Atividade 6 - Caderno do Aluno Volume 2 - Matrizes

Os exercícios devem ser  respondidos no Caderno do Aluno Volume 2 e enviar as imagens da atividade por e-mail até 01/07 para o e-mail jociener@prof.educacao.sp.gov.br

Habilidade: Compreender o significado das matrizes e das operações entre elas na representação de tabelas e de transformações geométricas no plano.

Recomendações: 

Assistir às aulas relacionadas aos links a seguir para e resolver os exercícios propostos.

22/06 - 2ª série EM - Matemática - Aplicação de matrizes: Parte III: https://youtu.be/y1DYR0lCGyo

 

1.      1. Na representação a seguir, de um plano cartesiano, podemos observar três triângulos congruentes. O triângulo ABC pode ser transladado até coincidir com o triângulo DEF, que, por sua vez, se transladado, poderá coincidir com o triângulo GHI.

a)      Quantas unidades horizontais e quantas unidades verticais são necessárias para uma translação do triângulo ABC, a fim de que, ao final, ele coincida com o triângulo DEF?

b)      Quantas unidades horizontais e quantas unidades verticais são necessárias para uma translação do triângulo DEF, a fim de que, ao final, ele coincida com o triângulo GHI?

c)      Quantas unidades horizontais e quantas unidades verticais são necessárias para uma translação do triângulo ABC, a fim de que, ao final, ele coincida com o triângulo GHI?

d)      Escreva uma matriz 3x2 para cada triângulo, de maneira que cada linha da matriz contenha coordenadas de um vértice do triângulo, com a abscissa na   primeira coluna e a ordenada na segunda coluna.  Denomine a matriz referente ao triângulo ABC pela letra M, a matriz referente ao triângulo DEF pela letra N, e a matriz referente ao triângulo GHI pela letra P.

e)      Escreva uma matriz Q, tal que M + Q = N.

f)       Escreva uma matriz R, tal que N + R = P.

g)      Escreva uma matriz T, tal que M + T = P

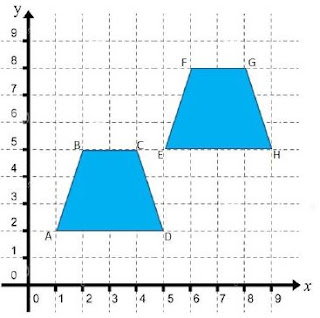
1.   2.  Observe os dois polígonos, ABCD e EFGH, apresentados no plano cartesiano. O EFGH é uma translação do ABCD, após duas movimentações, uma na horizontal e uma na vertical.

a)      Quantas unidades na horizontal e na vertical o polígono ABCD deverá se deslocar para coincidir com o EFGH?

b)      Componha a matriz P(4x2) com as coordenadas dos vértices do polígono ABCD e a matriz Q(4x2) com aquelas dos vértices do polígono EFGH, em que cada linha contenha a abscissa na primeira coluna e a ordenada na segunda.

c)      Escreva a matriz R(4x2), tal que P+R=Q.

3.  Observe os dois polígonos, ABCD e EFGH, apresentados no plano cartesiano. 

  a) Quantas unidades na horizontal e na vertical do polígono ABCD deverão ser deslocadas para, ao final, coincidirem com o EFGH?

b)  Represente em uma matriz A(4x2) as coordenadas dos vértices do polígono ABCD, de maneira que cada linha contenha coordenadas de um ponto com a abscissa na primeira coluna e a ordenada na segunda.

c)  Represente em uma matriz B(4x2) as coordenadas dos vértices do polígono EFGH, de maneira que cada linha contenha coordenadas de um ponto com a abscissa na primeira coluna e a ordenada na segunda.

d) Escreva uma matriz C(4x2), de tal forma que: A + C = B.