Impulso e quantidade de movimento.

 Recomendações aos alunos.

* Leiam o texto com atenção.
* Assistam às aulas pelo CMSP, TV, vídeo aulas pela plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.
* Identifiquem as atividades com o nome, série e n° de chamada ( se possível ), título da atividade e data de postagem no Blog.
* As atividades deverão ser enviadas para o e-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até  10/11.

Olá pessoal! Que todos estejam bem.

Nessa semana vamos estudar impulso e quantidade de movimento, para aprofundar o conhecimento a respeito dos movimentos.

* IMPULSO.

Como já vimos, para que um corpo entre em movimento, é necessário que haja um interação entre dois corpos.

Se considerarmos o tempo que esta interação acontece, teremos o corpo sob ação de uma força constante, durante um intervalo de tempo muito pequeno, este será o impulso de um corpo sobre o outro:

As características do impulso são:

• Módulo: 
• Direção: a mesma do vetor F.
• Sentido: o mesmo do vetor F.

A unidade utilizada para Impulso, no SI, é: N.s

No gráfico de uma força constante, o valor do impulso é numericamente igual à área entre o intervalo de tempo de interação:

A = F.Δt = I

* QUANTIDADE DE MOVIMENTO.

Se observarmos uma partida de bilhar, veremos que uma bolinha transfere seu movimento totalmente ou parcialmente para outra.

A grandeza física que torna possível estudar estas transferências de movimento é a quantidade de movimento linear , também conhecido como quantidade de movimento ou momentum linear.

A quantidade de movimento relaciona a massa de um corpo com sua velocidade:

Como características da quantidade de movimento temos:

• Módulo: 
• Direção: a mesma da velocidade.
• Sentido: a mesma da velocidade.
• Unidade no SI: kg.m/s.

Exemplo:

1) Qual a quantidade de movimento de um corpo de massa 2kg a uma velocidade de 1m/s?

Teorema do Impulso

Considerando a 2ª Lei de Newton:

E utilizando-a no intervalo do tempo de interação:

mas sabemos que: , logo:

Como vimos:

então:

"O impulso de uma força, devido à sua aplicação em certo intervalo de tempo, é igual a variação da quantidade de movimento do corpo ocorrida neste mesmo intervalo de tempo."

Exemplo:

2) Quanto tempo deve agir uma força de intensidade 100N sobre um corpo de massa igual a 20kg, para que sua velocidade passe de 5m/s para 15m/s?

* CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO.

Assim como a energia mecânica, a quantidade de movimento também é mantida quando não há forças dissipativas, ou seja, o sistema é conservativo, fechado ou mecanicamente isolado.

Um sistema é conservativo se:

Então, se o sistema é conservativo temos:

Como a massa de um corpo, ou mesmo de um sistema, dificilmente varia, o que sofre alteração é a velocidade deles.

Exemplo:

3) Um corpo de massa 4kg, se desloca com velocidade constante igual a 10m/s. Um outro corpo de massa 5kg é lançado com velocidade constante de 20m/s em direção ao outro bloco. Quando os dois se chocarem ficarão presos por um velcro colocado em suas extremidades. Qual será a velocidade que os corpos unidos terão?

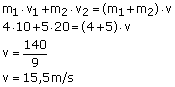
* COLISÕES OU CHOQUES MECÂNICOS.

Numa colisão  mecânica de dois corpos, sempre há trocas de forças internas. Mesmo que haja trocas de forças externas, estas são, normalmente, desprezíveis comparadas com as forças internas. Portanto, numa colisão de dois corpos, as forças externas são desprezíveis e as forças internas do sistema determinam uma resultante nula.

As colisões podem ser consideradas mecanicamente isoladas, ou seja, a quantidade de movimento do sistema de corpos permanece constante antes e depois do choque.

Colisões

Numa superfície plana e horizontal, dois corpos movendo-se com determinada velocidade sofrem uma colisão frontal e central. Nessa colisão, o sistema é considerado mecanicamente isolado tendo em vista que a quantidade de movimento do sistema mantém-se constante.

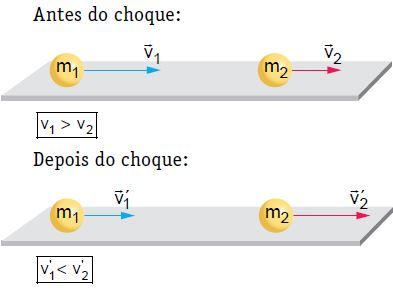
No nosso exemplo, depois do choque, o corpo 2 é impulsionado e tem sua velocidade elevada. Já o corpo 1 pode seguir no mesmo sentido que tinha antes do choque, porém com menor velocidade, parar ou retornar, ou seja, inverter o sentido do seu movimento. Para trabalhar a teoria, consideremos uma das situações, ou seja, aquela em que o corpo 1 segue no mesmo sentido que possuía antes do choque.

Para o sistema formado pelos dois corpos:

Q_antes = Q_depois
m₁ · v₁ + m₂ · v₂ = m₁ · v’₁ + m₂ · v’₂

Para colisões mecânicas unidirecionais (numa única direção), devemos adotar um sentido de orientação para o movimento e usar os sinais v > 0 para velocidade a favor da orientação e v < 0 para velocidade contrária à orientação.

Na equação acima, geralmente não são co­nhecidas as velocidades v’₁ e v’₂‘. Portanto, te­mos uma equação com duas incógnitas. Preci­samos de mais uma equação, a do coeficiente de restituição.

Coeficiente de restituição

Para que haja colisão, os corpos 1 e 2, antes do choque, aproximam-se com velocidade relativa v_{aproximação}.

v_{aproximação} = v₁ – v₂

Depois do choque, os corpos 1 e 2 se afas­tam com velocidade relativa v_afastamento.

v_afastamento = v’₂ − v’₁

O coeficiente de restituição (e) de um choque central e direto é um número adimensional que está associado à energia dissipada na colisão. Ele é obtido pela razão entre os módulos das velocidades de afastamento e aproximação.

Tipos de colisões mecânicas

Como na natureza não é possível criar nem destruir energia, então, numa colisão, a energia mecânica do sistema pode permanecer constante ou diminuir se houver dissipação na forma de calor, deformação e som.

Nessas condições, podemos escrever que a velocidade relativa de afastamento dos corpos, em módulo, é sempre menor ou igual ao módulo da velocidade relativa de aproximação dos corpos.

Colisão inelástica ou perfeitamente inelástica

É o tipo de choque em que, após a colisão, os corpos seguem juntos (com a mesma velocidade). Nesse caso, temos:

v_afastamento = 0
v’₂ = v’₁
e = 0

Na colisão inelástica, a energia cinética do sistema diminui, ou seja, parte da energia mecânica inicial do sistema é transformada em outras formas de energia. Esse tipo de choque é aquele que mais dissipa energia.

E_{c após} << E_c antes

Colisão parcialmente elástica ou parcialmente inelástica

Nesse choque, depois da colisão, os corpos seguem separados, ou seja, com velocidades diferentes, e o sistema perde uma parte da energia mecânica.

v’₂ ≠ v’₁
v_afastamento ≠ 0
0 < e < 1

Na colisão parcialmente elástica energia cinética do sistema diminui.

E_{c após} < E_c antes

Colisão perfeitamente elástica ou colisão elástica

Nesse choque, depois da colisão, os corpos seguem separados, ou seja, com velocidades diferentes, e o sistema não perde energia mecânica. Os corpos afastam-se com a mesma velocidade relativa com que se aproximam.

v’₂ ≠ v’₁
v_afastamento = v_{aproximação}
e = 1

Na colisão perfeitamente elástica a energia cinética do sistema permanece constante.

E_{c após} = E_c antes

Resumo

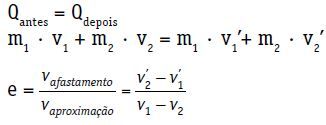
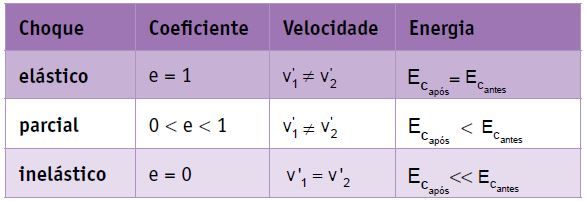
Numa colisão perfeitamente elástica de dois corpos de mesma massa, as velocidades sofrem permutação, ou seja, a velocidade final do corpo 1 é igual à velocidade inicial do corpo 2 e a velocidade final do corpo 2 é igual à inicial do corpo 1.

EXEMPLOS.

4) Um carrinho de massa m1 = 2,0 kg, deslocando-se com velocidade V1 = 6,0 m/s sobre um trilho horizontal sem atrito, colide com outro carrinho de massa m2 = 4,0 kg, inicialmente em repouso sobre o trilho. Após a colisão, os dois carrinhos se deslocam ligados um ao outro sobre esse mesmo trilho. Qual a perda de energia mecânica na colisão?

Resolução:

Q antes = Q depois

m1. v1 + m2 . v2 = (m1 + m2) . v'

2 . 6 + 4 . 0 = (2 + 4) . v'

12 + 0 = 6 .v'

12/6 = v'

v' = 2 m/s

Ec antes = m1 . v1²/2

Ec antes = 2 . 6²/2

Ec antes = 2 . 36/2

Ec antes = 72/2

Ec antes = 36 J

Ec depois = (m1 + m2) . v'²/2

Ec depois = (2 + 4) . 2²/2

Ec depois = 6 . 4/2

Ec depois = 24/2

Ec depois = 12 J

Portanto, a perda de energia é:

E dissipada = Ec antes - Ec depois

E dissipada = 36 - 12

E dissipada = 24 J

5) Em um clássico do futebol goiano, um jogador do Vila Nova dá um chute em uma bola aplicando-lhe uma força de intensidade 7.10²N em 0,1s em direção ao gol do Goiás e o goleiro manifesta reação de defesa ao chute, mas a bola entra para o delírio da torcida. Determine a intensidade do impulso do chute que o jogador dá na bola para fazer o gol.

Resolução:

I = F . Δt

I = 7.10² . 0,1

I = 0.7.10²

I = 70 N.s

6) Sobre uma partícula de 8 kg, movendo-se à 25m/s, passa a atuar uma força constante de intensidade 2,0.10²N durante 3s no mesmo sentido do movimento. Determine a quantidade de movimento desta partícula após o término da ação da força.

Resolução:

I = ΔQ

F . Δt = Q - Qo

2.10² . 3 = Q - m . Vo

6.10² = Q - 8 . 25

600 = Q - 200

600 + 200 = Q

Q = 800 Kg.m/s

ASSISTAM A VÍDEO AULA COM O PROFESSOR MARCELO BOARO, ATRAVÉS DO LINK:

https://youtu.be/qXfu31IC8Q4

VÍDEO DISPONÍVEL NO YOUTUBE.

Agora façam aos exercícios que seguem.

Bons estudos!

EXERCÍCIOS.

1) Pular corda é uma atividade que complementa o condicionamento físico de muitos atletas. Suponha que um boxeador exerça no chão uma força média de 1,0 x 104 N, ao se erguer pulando corda. Em cada pulo, ele fica em contato com o chão por 2,0 x 10-2 s.

Na situação dada, o impulso que o chão exerce sobre o boxeador, a cada pulo, é:

a) 4.10² N.s

b) 3.10² N.s

c) 2.10² N.s

d) 1.10² N.s

e) 3.10³ N.s

2) Admita uma colisão frontal totalmente inelástica entre um objeto que se move com velocidade inicial Vo e outro objeto inicialmente em repouso, ambos com mesma massa.

Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão equivale a:

a) Vo/2

b) Vo/4

c) 2.Vo

d) 4.Vo

e) Vo

3) No futebol, o pênalti é a penalidade máxima para a equipe. A bola é colocada na linha de grande penalidade, a 11 m do ponto médio entre as traves (no centro da meia-lua, em frente à baliza) e o duelo trava-se unicamente entre o rematador e o goleiro. Imediatamente após a cobrança do pênalti, o jogo prossegue naturalmente, o que significa que se o goleiro defender a bola para longe da baliza, isto é, não a agarre, os jogadores, que esperam atrás da linha de remate, podem continuar a jogar e insistir no remate.

Uma bola de futebol está em repouso na marca do pênalti. O árbitro autoriza a cobrança. O jogador chuta a bola, que tem aproximadamente 0,50 kg de massa. O toque do pé do jogador sobre a bola atua por 0,20 s e ela adquire velocidade de 72 km/h.

Não considerando possíveis perdas, a intensidade da força média que o pé do jogador faz sobre a bola é, em Newton, igual a:

a) 20 N

b) 30 N

c) 40 N

d) 50 N

e) 60 N

4) Dois veículos, A e B, de massas iguais a 1.000 kg e 800 kg, respectivamente, colidem frontalmente. A velocidade do veículo A era de 40 km/h no momento da colisão. 

Considerando-se a situação acima, para que os veículos ficassem parados após a colisão, a velocidade do veículo B (em módulo) deveria ser igual a:

a) 10 Km/h

b) 20 Km/h

c) 30 Km/h

d) 40 Km/h 

e) 50 Km/h

5) Quanto tempo deve agir uma força de intensidade 3.10² N sobre um corpo de massa igual a 10kg, para que sua velocidade passe de 2 m/s para 14m/s?

a) 0,3 s

b) 0,4 s

c) 0,1 s

d) 0,2 s

e) 0,5 s