S.E.I. (Semana de Estudos Intensivos): Lançamentos verticais e oblíquos.

  Recomendações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 20/10.

Olá pessoal! Que todos estejam bem.

Nessa semana de estudos intensivos, vamos rever os lançamentos verticais e oblíquos que ocorrem na superfície da Terra.

Lançamentos Verticais.

Um corpo lançado verticalmente para cima, sobe até uma determinada altura, para e começa a cair.

Durante a subida o movimento é retardado, pois a velocidade diminui até parar, pois a aceleração da gravidade é orientada para baixo, sendo contrária ao movimento e portanto seu valor é negativo durante a subida do corpo (g = -10 m/s²).

Durante a descida, o movimento é acelerado, pois a aceleração e a velocidade têm o mesmo sentido     (g = 10 m/s²).

Para o lançamento vertical são usadas as equações do MUV.

* Função horária das velocidades: V = Vo + a . t, sendo a = g.

* Função horária das posições: S = So + Vo.t + a/2 . t²

* Equação de Torricelli: V² = Vo² + 2. a . ΔS

Desconsiderando a resistência do ar, todos os corpos, independentemente de sua massa caem com a mesma velocidade. O tempo em que o corpo leva para atingir a altura máxima é igual ao tempo em que o corpo leva para cair até o ponto de lançamento. Assim, conclui-se que: ts = td.

ts: tempo de subida

td = tempo de descida

A altura máxima atingida pelo corpo é calculada por : Hmax = Vo²/2.g

 Fatos empíricos mostram que um corpo próximo da superfície da terra ou de qualquer astro sofre uma atração, constante vertical e para baixo, chamada aceleração da gravidade local (g), para simplificar será considerada sempre constante na superfície de um determinado local.

Próximo a superfície terrestre um corpo é lançado verticalmente para cima, este corpo tem uma Vo e p está sujeito a uma aceleração constante g (valor absoluto da gravidade local).

Neste trecho do movimento o corpo irá subir verticalmente para cima sujeito a uma aceleração (g) vertical para baixo, assim pode-se considerar que sua aceleração (a): a = -g (sinal negativo representa que são em direções opostas).
Para o estudo deste movimento é claro que estaremos tratando de um movimento uniformemente variado.

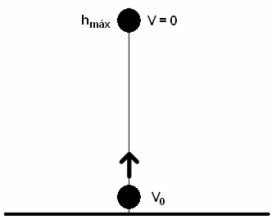
Assim, iremos estuda-lo pelas equações do MUV.

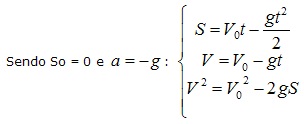
Fatos importantes
No topo da trajetória a sua velocidade é nula (ponto de inversão de movimento)
Após atingir o topo de sua trajetória este corpo irá sofrer uma queda livre onde a=g. Mostremos que o tempo de subida é igual ao tempo de queda t_s (tempo de subida)

Obs.: Ler sobre salto de paraquedas, onde devido à resistência do ar o paraquedista chega a uma velocidade máxima, a partir deste ponto seu movimento é praticamente uniforme (velocidade terminal).

O que cai mais rápido, uma bola de ferro ou uma pena?

O vídeo abaixo mostra um experimento muito interessante. No primeiro momento, uma pena e uma bola de ferro são soltas, ao mesmo tempo, em pressão atmosférica. Em razão do atrito com o ar, a pena leva mais tempo para tocar à mesa. Mas quando o experimento é repetido no vácuo, os dois objetos tocam a mesa no mesmo instante.

Lançamento Vertical para Cima

g é negativo

Como a gravidade aponta sempre para baixo, quando jogamos algo para cima, o movimento será acelerado negativamente, até parar em um ponto, o qual chamamos Altura Máxima.

Lançamento Vertical para Baixo

g é positivo

No lançamento vertical para baixo, tanto a gravidade como o deslocamento apontam para baixo. Logo, o movimento é acelerado positivamente. Recebe também o nome de queda livre.

Exemplo

1) Uma bola de futebol é chutada para cima com velocidade igual a 20m/s.
(a) Calcule quanto tempo a bola vai demorar para retornar ao solo.
(b) Qual a altura máxima atingida pela bola? Dado g=10m/s².

(a)

Neste exemplo, o movimento é uma combinação de um lançamento vertical para cima + um lançamento vertical para baixo (que neste caso também pode ser chamado de queda livre). Então, o mais indicado é calcularmos por partes:

Movimento para cima:

 

 

Movimento para baixo:

 

Como não estamos considerando a resistência do ar, a velocidade final será igual à velocidade com que a bola foi lançada.

 

Observamos, então, que nesta situação, onde a resistência do ar é desprezada, o tempo de subida é igual ao de decida.

 

(b)

Sabendo o tempo da subida e a velocidade de lançamento, podemos utilizar a função horária do deslocamento, ou então utilizar a Equação de Torricelli.

 

Lembre-se de que estamos considerando apenas a subida, então t=2s

 

ou

 

 

ou

Hmax = Vo²/2.g

Hmax = 20²/2.10

Hmax = 400/20

Hmax = 20 m

2) Uma pedra com massa 200 g é arremessada verticalmente para baixo com velocidade de5 m/s, de uma altura de 30 m. Adotando g = 10 m/s², responda:

a) qual a velocidade da pedra ao atingir o solo?

b) quanto tempo leva para a pedra atingir o solo?

Resolução:

Como a pedra é arremessada para baixo com velocidade de 5 m/s, a aceleração é positiva. Utilizando a equação de Torricelli, temos:

a)

V² = Vo² + 2.g.ΔS

V² = 5² + 2.10.30

V² = 25 + 600

V² = 625

V = ⎷625

V = 25 m/s

b) Aplicando a função horária das velocidades, temos:

V = Vo + g.t

25 = 5 + 10.t

25 - 5 = 10.t

20 = 10.t

20/10 = t

t = 2 s

* Lançamento oblíquo.

O lançamento oblíquo ocorre quando um objeto inicia seu movimento formando um determinado ângulo com a horizontal. Nesse tipo de lançamento, o objeto executa dois movimentos simultâneos, ao mesmo tempo em que executa um movimento na vertical, subindo e descendo, também se desloca horizontalmente.

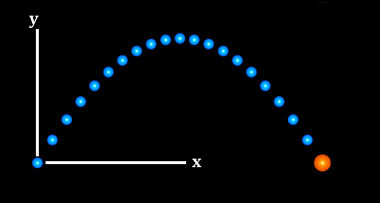
A imagem acima indica a trajetória de um corpo que executa um movimento oblíquo. Esses tipos de movimentos podem ser observados, por exemplo, no tiro de meta executado por um goleiro em uma partida de futebol, e no momento da tacada em uma bola de golfe.

A análise do lançamento oblíquo deve ser feita levando em consideração o movimento executado na vertical (eixo y) e o movimento na horizontal (eixo x). Quanto ao movimento no eixo y, a preocupação será a determinação da altura máxima atingida pelo corpo, por conta da atuação da gravidade neste eixo o movimento será uniformemente variado. As análises do movimento no eixo x irão determinar o alcance horizontal do lançamento, isto é, a distância entre os pontos de partida e chegada. Horizontalmente, o movimento será retilíneo e uniforme.

Mapa Mental: Lançamento Oblíquo

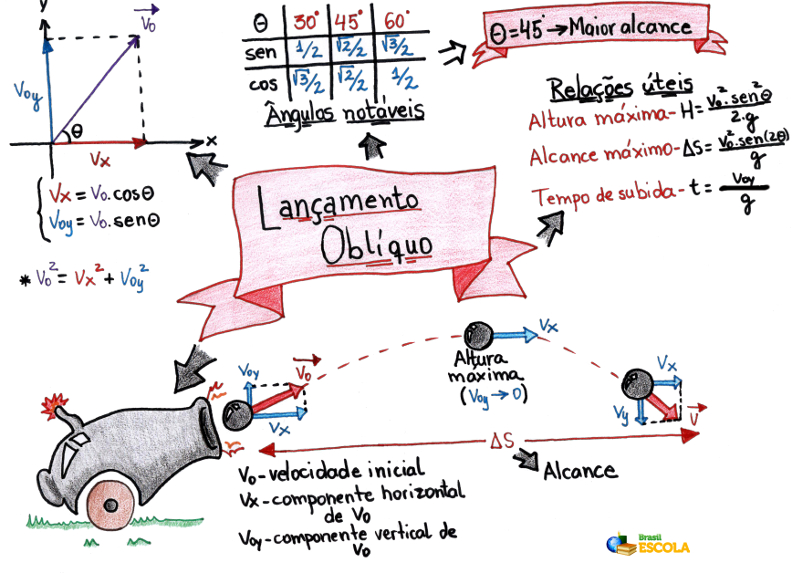
Alcance horizontal

O alcance horizontal é a distância entre os pontos de partida e chegada do objeto lançado obliquamente. A sua determinação será feita a partir da função horária da posição para o movimento retilíneo uniforme (MRU), sendo assim podemos escrever:

Observe que a diferença entre as posições final (s) e inicial (s₀) foi substituída por A, simbolizando o alcance do objeto. Perceba ainda que a velocidade utilizada foi uma componente no eixo x (V_X) da velocidade do objeto. A velocidade do objeto forma um ângulo θ com a horizontal, sendo assim, as análises feitas tanto na horizontal quanto na vertical devem utilizar os devidos componentes do vetor velocidade em cada eixo.

Eixo y: V_y = V.sen θ

Eixo x: V_x = V.cos θ

O tempo considerado na equação do alcance (A) é o tempo total para que o objeto saia do chão, atinja a altura máxima e retorne ao solo. No estudo do lançamento vertical, vemos que o tempo gasto para que um objeto atinja a altura máxima vertical é dado por:

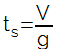
Nessa equação, V é a velocidade do objeto e g é a aceleração da gravidade. Para o caso do lançamento oblíquo, a velocidade considerada na vertical será a componente V_y, sendo assim, podemos escrever:

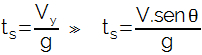
O tempo destacado acima refere-se à subida do objeto, logo, o tempo total do movimento será o dobro.

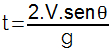
Assim, a equação do alcance poderá ser reescrita:

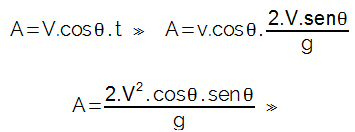
O termo 2.cosθ.senθ pode ser substituído pela identidade trigonométrica sen2θ, sendo assim, a equação final para a determinação do alcance horizontal em um lançamento oblíquo será:

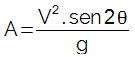
O alcance será o máximo possível quando o ângulo de lançamento for igual a 45°. Como o ângulo é multiplicado por dois na equação do alcance, o seno calculado será o de 90°, que corresponde ao máximo valor de seno possível, assim o alcance será o máximo possível.

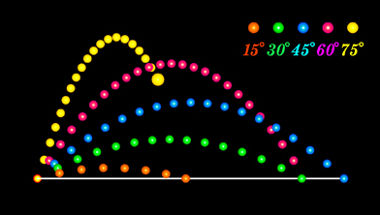
A imagem abaixo indica as possíveis trajetórias para lançamentos oblíquos executados sobre ângulos diversos. Observe que o maior alcance ocorre quando o ângulo de lançamento é igual a 45º.

Altura máxima

A altura máxima será determinada a partir da equação de Torricelli, equação do movimento uniformemente variado independente do tempo.

Para o lançamento oblíquo, teremos:

Na altura máxima, a velocidade do móvel será nula. O sinal negativo na equação acima justifica-se pelo fato do movimento ser acendente, contrário ao sentido da gravidade.

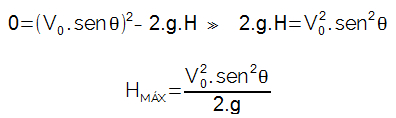
A equação acima determina a altura máxima atingida por um objeto que executa movimento oblíquo.

Exemplos.

Exemplo:

Um dardo é lançado com uma velocidade inicial v0=25m/s, formando um ângulo de 45° com a horizontal. (a) Qual o alcance máximo (b) e a altura máxima atingida?

Para calcular este movimento deve-se dividir o movimento em vertical e horizontal.

Para decompor o vetor em seus componentes são necessários alguns fundamentos de trigonometria:

Genericamente podemos chamar o ângulo formado de .

Então:

Substituindo os dados do problema na equação:

A = (Vo² . sen 2Θ)/g

b) Hmax = (Vo² . sen² Θ)/2.g

Hmax = (25² . sen² 45°)/2.10

Hmax = (625 . (⎷2/2)²)/20

Hmax = (625 . 0,5)/20

Hmax = 312,5/20

Hmax = 15,625 m.

Assistam as vídeo aulas pelos links:

https://youtu.be/14EHg91psHw

https://youtu.be/msU7g-aR3Iw

https://youtu.be/ryScqdbctFA

Todos os vídeos estão disponíveis no YouTube.

Agora façam os exercícios que seguem.

Exercícios.

1) Ao iniciar um jogo de basquete, o juiz jogou a bola verticalmente para cima com uma velocidade de 16 m/s. Adotando a aceleração da gravidade local como g = 10 m/s², qual a altura máxima atingida pela bola?

a) 10,2 m

b) 11,5 m

c) 12,8 m

d) 13,4 m 

e) 14 m

2) Se esse jogo acontecesse em Vênus, cuja aceleração da gravidade é g = 9 m/s², qual seria a altura máxima atingida pela bola?

a) 12 m

b) 14,2 m

c) 15 m

d) 16,4 m

e) 18,2 m

3) De um prédio de 25 andares, com 80 m de altura, é largada uma pedra com 200 g de massa. Adotando a aceleração da gravidade igual a g = 10 m/s², qual a velocidade da pedra ao atingir o solo?

a) 20 m/s

b) 25 m/s

c) 30 m/s

d) 40 m/s

e) 45 m/s

4) A bala de um canhão, com massa de 15 kg, é lançada com velocidade de 300 m/s. Determine o alcance horizontal máximo do projétil para o caso de o ângulo formado entre o canhão e a horizontal ser de 15°.

Dados: Sen 30° = 0,5

Gravidade = 10 m/s².

a) 2,5 km

b) 3,0 km

c) 3,5 km

d) 4,0 km

e) 4,5 km

5) As afirmações abaixo são a respeito do lançamento oblíquo.

I) O ângulo que fornecerá o maior alcance horizontal possível é o de 45°.

II) Ao chegar na altura máxima a componente vertical da velocidade do móvel é nula.

II) A componente horizontal da velocidade mantêm-se inalterada, uma vez que no eixo x o movimento é classificado como retilíneo e uniforme.

IV) A componente vertical da velocidade diminui desde o solo até se tornar nula na altura máxima, o que classifica o movimento como sendo acelerado.

V) A componente horizontal da velocidade pode ser determinada pelo produto da velocidade do objeto com o cosseno do ângulo com o qual o corpo abandona o solo.

Podemos afirmar que:

a) I, II, III e V estão corretas.

b) I,III, IV e V estão corretas.

c) I, II, III e IV estão corretas.

d) II, IV e V estão corretas.

e) Todas estão corretas.