Óptica geométrica: lentes esféricas e defeitos da visão.

 Orientações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 27/10.

Olá pessoal! Que todos estejam bem.

Nessa semana vamos estudar as lentes esféricas e os defeitos da visão.

As lentes esféricas fazem parte do estudo da física óptica, sendo um dispositivo óptico composto por três meios homogêneos e transparentes.

Nesse sistema, dois dioptros estão associados, sendo que um deles é necessariamente esférico. Já o outro dioptro, pode ser plano ou esférico.

As lentes possuem uma grande importância nas nossas vidas, posto que com elas podemos aumentar ou reduzir o tamanho de um objeto.

Exemplos

Muito objetos do cotidiano utilizam as lentes esféricas, por exemplo:

• Óculos
• Lupa
• Microscópios
• Telescópios
• Câmeras Fotográficas
• Filmadoras
• Projetores

Tipos de Lentes Esféricas

De acordo com a curvatura que apresentam, as lentes esféricas são classificadas em dois tipos:

Lentes Convergentes

Também chamadas de lentes convexas, as lentes convergentes apresentam uma curvatura para o exterior. O centro é mais espesso e a borda é mais delgada.

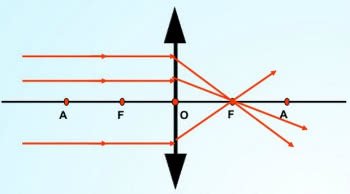
Esquema de lente convergente

O principal objetivo desse tipo de lente esférica é de aumentar os objetos. Recebem esse nome pois os raios de luz convergem, ou seja, se aproximam.

Lentes Divergentes

Também chamadas de lentes côncavas, as lentes divergentes apresentam uma curvatura interna. O centro é mais fino e a borda é mais espessa.

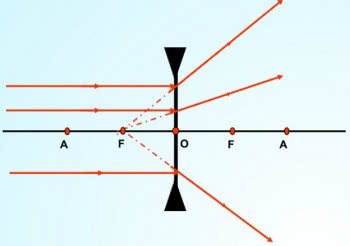
Esquema de lente divergente

O principal objetivo desse tipo de lente esférica é de diminuir os objetos. Recebem esse nome pois os raios de luz divergem, ou seja, afastam.

Além disso, segundo os tipos de dioptros que apresentam (esféricos ou esférico e plano), as lentes esféricas podem ser de seis tipos:

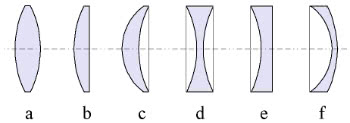
Tipos de Lentes Esféricas

Lentes Convergentes: bordas mais finas que o centro.

• a) Biconvexa: possui duas faces convexas
• b) Plano Convexa: uma face é plana, e o outra, convexa
• c) Côncavo-convexa: uma face é côncava, e o outra, convexa

Lentes Divergentes: bordas mais grossas que o centro.

• d) Bicôncava: possui duas faces côncavas
• e) Plano Côncava: uma face é plana, e a outra, côncava
• f) Convexa-Côncava: uma face é convexa, e a outra, côncava

Obs: Dentre esses tipos, três delas apresentam uma borda mais fina, e três bordas mais espessas.

Formação de Imagens

A formação de imagens varia de acordo com o tipo de lente:

Lente Convergente

As imagens podem ser formadas em cinco casos:

• Imagem real, invertida e menor do que o objeto (objeto localizado antes do foco antiprincipal).
• Imagem real, invertida e mesmo tamanho do objeto (objeto sobre o antiprincipal objeto).
• Imagem real, invertida e maior que o objeto (objeto localizado entre o foco antiprincipal e o foco objeto).
• Imagem imprópria (está no infinito) (objeto sobre o foco objeto)
• Imagem virtual, a direita do objeto e maior do que ele (objeto localizado entre o foco objeto e o centro óptico)

Lente divergente

Já a lente divergente, a formação de imagem é sempre: virtual, a direita do objeto e menor do que ele (objeto em qualquer posição).

Potência Focal ou vergência.

Cada lente apresenta uma potência focal, ou seja, a capacidade de convergir ou divergir os raios de luz. A potência focal é calculada pela fórmula:

P = 1/f

Sendo,

P: potência focal
f: distância focal (da lente ao foco)

No Sistema Internacional, a potência focal é medida em Dioptria (D) e a distância focal em metros (m).

Importante notar que nas lentes convergentes, a distância focal é positiva, por isso também são chamadas de lentes positivas. Já nas lentes divergentes ela é negativa, e portanto, são chamadas de lentes negativas.

Elementos geométricos das lentes esféricas

Toda lente esférica, seja ela côncava, seja convexa, apresenta elementos geométricos em comum, sendo eles:

• centro óptico (O);

• foco principal objeto e foco principal imagem (F e F');

• foco antiprincipal objeto e foco antiprincipal imagem, também conhecidos como centros de curvatura no caso dos espelhos esféricos (A e A' ou C e C').

A figura a seguir mostra onde ficam os elementos geométricos de uma lente esférica qualquer, observe:

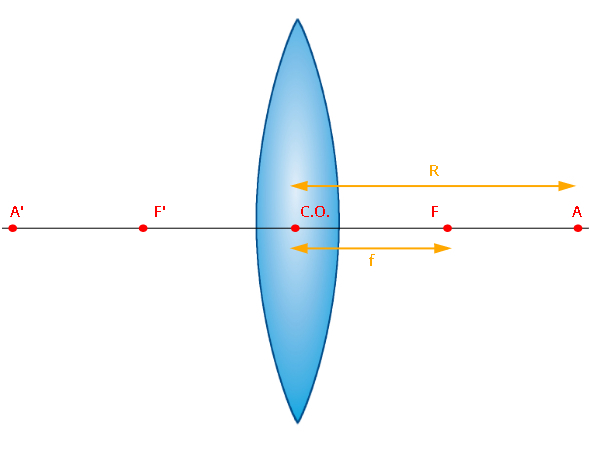
Com base na imagem acima, dizemos que a distância entre o centro óptico da lente e o foco principal objeto é chamada de distância focal (f); do mesmo modo, a distância entre o centro óptico e o foco antiprincipal objeto é chamado de raio de curvatura.

Na figura acima, também é possível observar uma linha horizontal que separa a lente em duas partes. Essa linha é chamada de eixo de simetria e é a partir dela que é construído o referencial de Gauss, usado para definir a convenção de sinais das lentes esféricas. De acordo com o referencial de Gauss:

• qualquer ponto ou elemento que esteja localizado acima do eixo de simetria possui sinal positivo;
• qualquer ponto ou elemento localizado abaixo do eixo de simetria possui sinal negativo;
• qualquer ponto ou elemento localizado à direita do centro óptico da lente possui sinal positivo;
• qualquer ponto ou elemento localizado à esquerda do centro óptico da lente possui sinal negativo.

A figura a seguir nos auxiliará a entender a convenção de sinais segundo o referencial de Gauss. Confira:

Referencial de Gauss para lentes esféricas

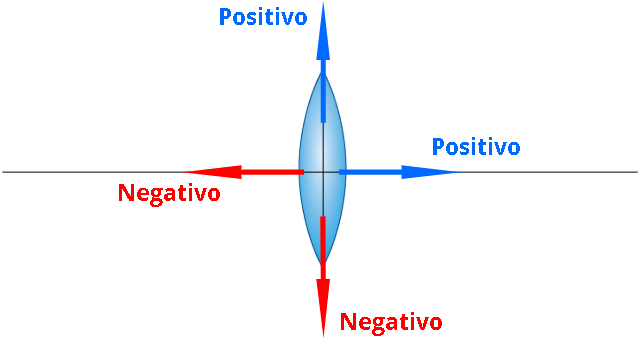
Além das convenções arbitradas pelo referencial de Gauss, há algumas informações úteis que podem ser levadas em conta na hora de resolver exercícios. Tanto o foco principal quanto o foco antiprincipal das lentes divergentes, como as lentes côncavas, são negativos. Além disso, quando o tamanho da imagem (i) tiver o sinal negativo, isso indicará que ela está invertida. Por fim, se descobrirmos que a posição de uma imagem (p') é positiva, isso indica que essa imagem é real; do contrário, se a posição da imagem fosse negativa, essa imagem seria virtual.

Raios notáveis

Os raios notáveis são necessários para entendermos como funciona a formação de imagens nas lentes esféricas. Trata-se de raios de luz que sempre são refratados sobre certos elementos geométricos específicos das lentes esféricas. Além disso, faz-se necessário relembrar um dos princípios da óptica geométrica: a reversibilidade dos raios de luz. Quando desenhamos um raio de luz indo de um ponto a outro, esse raio tanto pode estar fazendo o caminho de “ida” quanto o de caminho “volta”.

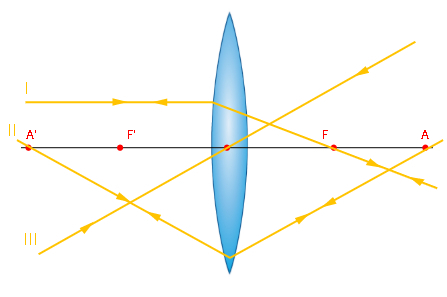
De acordo com a imagem acima, todo raio de luz que:

• I - incide paralelamente ao eixo de simetria é refratado em cima do foco principal (F); / incide sobre o foco principal é refratado paralelamente ao eixo de simetria.
• II - incide sobre o foco antiprincipal objeto (A) é refratado sobre o foco principal imagem (A'); / incide sobre o foco antiprincipal imagem (A') é refratado sobre o foco antiprincipal objeto (A).
• III- incide sobre o centro óptico é refratado sem sofrer nenhum desvio lateral.

Formação de imagens nas lentes esféricas

A formação de imagens nas lentes esféricas exige que tracemos os raios de luz notáveis que são refratados através da lente. A imagem é sempre formada no ponto onde dois raios de luz refratados se cruzam. Quando a imagem é formada do mesmo lado que o objeto, essa imagem é qualificada como virtual; quando a imagem for formada no lado da lente oposto ao objeto, será real.

Confira aqui quais são as características das imagens reais e virtuais:

• Imagem real: pode ser projetada, é invertida e formada pelo cruzamento de pelo menos dois raios de luz.

• Imagem virtual: toda imagem virtual não pode ser projetada, é direita e formada pelo cruzamento de prolongamentos dos raios de luz.

Além disso, a formação de imagens nas lentes esféricas depende da posição do objeto em relação ao centro óptico da lente e também do formato da lente, que tanto pode ser côncava quanto convexa. Para as lentes côncavas, só há um caso de formação de imagem: todas as imagens formadas por lentes côncavas são virtuais, formadas pelo cruzamento de prolongamentos de raios de luz e sempre menores que o objeto da imagem.

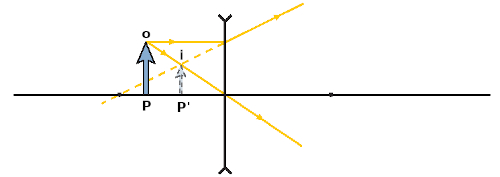
p e p' – posições do objeto e da imagem

o – altura do objeto

i – altura da imagem

No caso das lentes de bordas finas, a formação de imagens é mais complexa e envolve um total de cinco casos. Vamos analisá-los um a um, começando pela situação em que um objeto está distante da lente e de seu foco antiprincipal. Nesse caso, a imagem formada é invertida, real, formada pelo cruzamento dos raios de luz e menor que o objeto.

Imagem real, invertida e reduzida

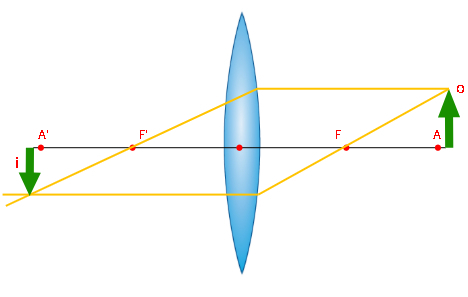
Quando o objeto é aproximado da lente e é colocado exatamente sobre o foco antiprincipal, a imagem formada é real, invertida e de mesmo tamanho que o objeto. Observe:

Imagem real, invertida e de mesmo tamanho

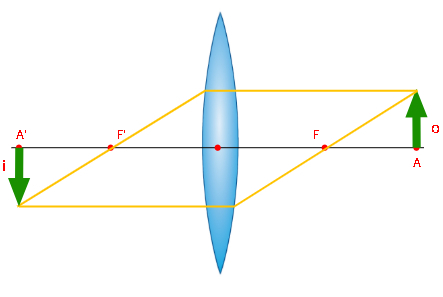
Aproximando o objeto um pouco mais em relação à lente, ele ficará entre o foco antiprincipal e principal, respectivamente. Nesse caso, a imagem conjugada pela lente será real, invertida e cada vez maior, de acordo com a aproximação.

Imagem real, invertida e ampliada

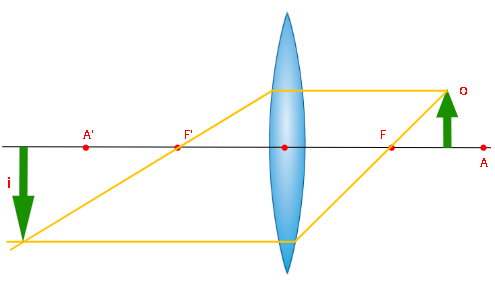
Quando o objeto é colocado a uma distância do centro óptico da lente convexa que coincide com sua distância focal, ou seja, quando o objeto é disposto em cima do foco principal, não há formação de imagem, uma vez que os raios de luz refratados pela lente são paralelos e, portanto, não se cruzam. Nesse caso, dizemos que a imagem é imprópria e que é formada no infinito.

Imagem imprópria e formada no infinito

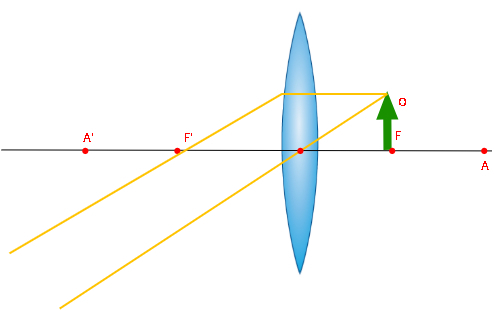
O último caso é aquele em que o objeto é colocado próximo da lente convexa, entre o foco principal e o centro óptico. Nesse caso, os raios de luz refratados são divergentes, por isso a imagem formada é virtual, formada pelo cruzamento de prolongamentos de raios de luz e maior que o objeto.

Legenda

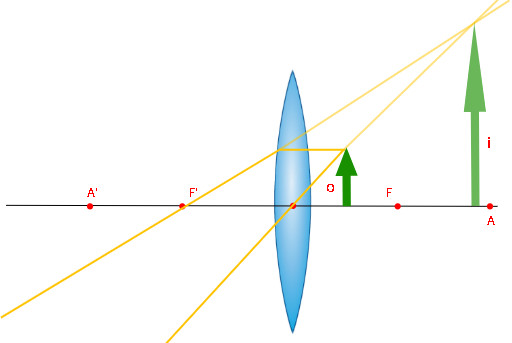
Vergência, dioptria e justaposição de lentes esféricas

Vergência é a medida da capacidade de uma lente de desviar a trajetória da luz. É simbolizada pela letra C, e sua unidade de medida é a dioptria (di), que equivale a m^-1. Uma vergência positiva indica que a lente é convergente, enquanto uma vergência negativa indica que ela é divergente. A vergência de uma lente pode ser facilmente calculada se soubermos a distância focal da lente.

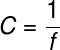
Justaposição de lentes esféricas

A justaposição de lentes esféricas é o processo de combinar diferentes lentes, de modo a se obter distintas configurações de vergência. Além disso, esse processo é usado para reduzir um efeito chamado de aberração cromática, mas também pode ser usado para aumentar o efeito obtido por uma única lente.

A aberração cromática acontece quando a luz percorre um grande caminho no interior de uma lente, fazendo com que a luz refratada pela lente sofra dispersão, separando, assim, suas componentes, assim como ocorre com a luz que passa através de um prisma.

A figura a seguir mostra a justaposição de duas lentes esféricas de vergências C₁ e C₂. A vergência equivalente dessa combinação é igual à soma das vergências individuais.

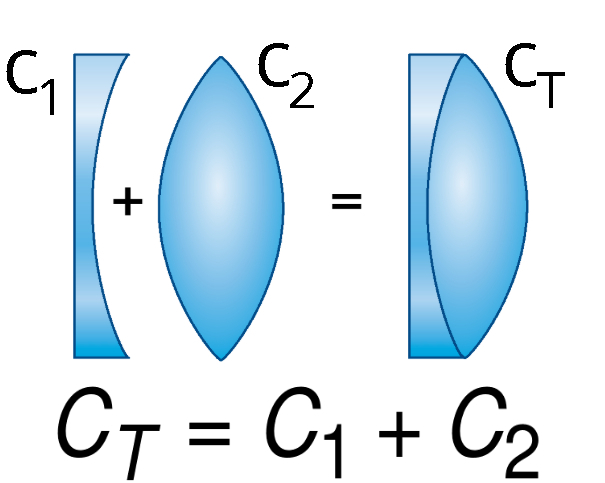
Fórmulas das lentes esféricas

As principais fórmulas usadas para resolver exercícios sobre as lentes esféricas utilizam as variáveis:

• f – distância focal;
• p e p' – posição do objeto e da imagem;
• o – tamanho do objeto;
• i – tamanho da imagem;
• A – aumento linear transversal ou ampliação;
• R – raio de curvatura;
• C – vergência.

A unidade de medida da vergência ou potência focal é a dioptria (D).

A fórmula mais básica das lentes esféricas é conhecida como aumento linear transversal ou ampliação. A ampliação da lente pode ser calculada por meio de três fórmulas diferentes, que podem ser combinadas entre si. Confira:

Além da fórmula acima, há também uma fórmula conhecida como equação dos pontos conjugados ou equação de Gauss. Veja:

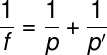
A fórmula a seguir é utilizada para calcular a vergência ou o grau das lentes esféricas:

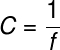
Por fim, a fórmula a seguir, conhecida como equação de Halley ou equação do fabricante de lentes, é utilizada para determinar a vergência de uma lente esférica com base no índice de refração do material da lente e do meio em que a lente encontra-se imersa (ar, por exemplo), além dos raios de curvatura das faces externa e interna da lente. Confira:

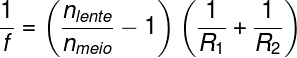
Exemplos

1. Qual a potência focal ou a vergência de uma lente convergente de distância focal de 0,10 metros?

P = 1/f
P = 1/0,10
P = 10 D

2. Qual a potência focal de uma lente divergente de distância focal de 0,20 metros?

Resolução:

Como se trata de uma lente divergente, a distância focal é negativa.

P = 1/f
P = 1/-0,20
P = - 5 D

3) Um objeto real é colocado perpendicularmente ao eixo principal de uma lente convergente de distância focal f. Se o objeto está a uma distância 3f da lente, a distância entre o objeto e a imagem conjugada por essa lente é:

Resolução:

Aplicando a equação de Gauss, temos:

1/f = 1/p +1/p'

1/f = 1/3f + 1/p'   ( mmc entre 3f e p' é 3fp'. Divide pelo de baixo e multiplica pelo de cima)

1/f = p' + 3f/3fp'   (passa o 3fp' multiplicando)

3fp'/f = 3f + p'      (cancela f com f)

3p' = 3f + p'        (isolando p')

3p' - p' = 3f

2p' = 3f

p' = 3f/2

4) Um objeto tem altura h_o = 20 cm e está localizado a uma distância d_o = 30 cm de uma lente. Esse objeto produz uma imagem virtual de altura h_i = 4,0 cm. A distância da imagem à lente, a distância focal e o tipo da lente são, respectivamente:

a) 6,0 cm; 7,5 cm; convergente;

b) 1,7 cm; 30 cm; divergente;

c) 6,0 cm; -7,5 cm; divergente;

d) 6,0 cm; 5,0 cm; divergente;

e) 1,7 cm; -5,0 cm; convergente.

Resolução:

A distância da imagem à lente é calculada por:

i/o = -p'/p

4/20 = -p'/30

4 . 30 = -p' . 20

120/20 = -p'

-p' = 6

p' = -6 cm. Como p' é negativo, a lente é divergente.

A distância focal é calculada por:

1/f = 1/p + 1/p'

1/f = 1/30 + 1/-6

1/f = 1/30 - 1/6    (mmc(30 , 6)=30. Divide pelo de baixo e multiplica pelo de cima)

1/f = 1 - 5/30

1/f = -4/30

30 = -4f

30/-4 = f

f = -7,5 cm (como f é negativo, a lente é divergente)

Resposta: C

DEFEITOS DA VISÃO

O olho humano pode apresentar algumas anormalidades que levam a dificuldades de enxergar em algumas situações.
Essas anormalidades podem ser: Miopia, Hipermetropia, Astigmatismo, Presbiopia e Estrabismo.

Estudaremos agora essas disfunções do globo ocular e qual o melhor método de correção desses problemas.

Miopia

É uma anomalia da visão que consiste em um alongamento do globo ocular.
Nesse caso há um afastamento da retina em relação ao cristalino, fazendo que a imagem seja formada antes da retina, tornando-a não nítida.
Para o míope, o ponto próximo (ou remoto), que é o ponto onde a imagem é nítida, está a uma distância finita, maior ou menor, conforme o grau da miopia.
O míope tem grandes dificuldades de enxergar objetos distantes.
A correção da miopia é feita comumente com a utilização de lentes divergentes. Ela fornece, de um objeto impróprio (objeto no infinito), uma imagem virtual no ponto remoto do olho. Essa imagem se comporta como objeto para o cristalino, produzindo uma imagem final real exatamente sobre a retina. 

 

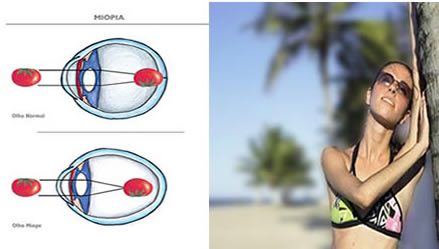
À Esquerda, esquema do olho míope. À direita, visão do míope.

 
Hipermetropia

A hipermetropia é um defeito oposto à miopia, ou seja, aqui existe uma diminuição do globo ocular.
Nesse caso a imagem de objetos próximos é formada além da retina, fazendo aquelas imagens não sejam formadas com nitidez.
A correção desse defeito é possível através da utilização de uma lente convergente. Tal lente convergente deve fornecer, de um objeto real, situado em um ponto próximo do olho, uma imagem que se comporta como objeto real para o olho, dando uma imagem final nítida. 

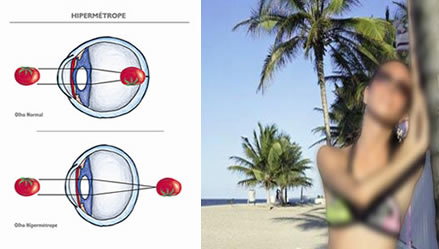
À esquerda, esquema do olho do Hipermétrope. À direita, a visão do hipermétrope

 

Astigmatismo

Consiste no fato de que as superfícies que compõem o globo ocular apresentam diferentes raios de curvatura, ocasionando uma falta de simetria de revolução em torno do eixo óptico.
A correção é feita com a utilização de lentes cilíndricas capazes de compensar tais diferenças entre os raios de curvatura.

Visão com astigmatismo

Presbiopia

Anomalia da visão semelhante à hipermetropia, que ocorre com o envelhecimento da pessoa, ocasionando o relaxamento dos músculos.
Porém, se a acomodação muscular for muito grande, o presbíope também terá problemas de visão a longa distância, uma vez que com a aproximação do ponto remoto, o problema se torna semelhante ao da miopia.
A correção nesse caso se dá com a utilização de lentes bifocais (convergentes e divergentes).

Estrabismo

Tal anomalia consiste no desvio do eixo óptico do globo ocular, a correção é feita com o uso de lentes prismáticas.

Assistam a vídeo aula do Professor Marcelo Boaro, através do link:

https://youtu.be/sJTrdArAeKY

Vídeo disponível no YouTube.

Agora façam os exercícios que seguem.

Bons estudos!

Exercícios.

1) Um objeto é colocado a 60 cm de uma lente esférica convergente. Tal lente possui distância focal igual a 20 cm. Calcule a distância da imagem à lente.

a) 20 cm

b) 30 cm

c) 40 cm

d) 50 cm

e) 60 cm

2) A grandeza física vergência é medida em dioptrias, o que, no cotidiano, é o “grau” de uma lente. Logo, uma pessoa que usa um óculo com lente para a correção de sua visão de 2,5 graus, está usando um óculo com uma lente de vergência igual a 2,5 dioptrias.

Essa lente tem uma distância focal de:

a) 0,25 m

b) 2,5 m

c) 0,3 m

d) 0,4 m

e) 1,25 m

3) Um oftalmologista receita óculos para uma pessoa hipermétrope, indicando que ela deve usar “lentes de 2,0 graus”. Fisicamente, isso significa que o valor da convergência das lentes deve ser 2,0 dioptrias.

Pode-se concluir que as lentes desses óculos devem ser:

a) divergentes, com 50 cm de distância focal.

b) divergentes, com 2,0 m de distância focal.

c) convergente, com 50 cm de distância focal.

d) convergentes, com 2,0 m de distância focal.

e) convergente, com 5,0 m de distância focal.

4) Ao pegar os óculos de Gustavo, Fabiana percebeu que estes forneciam uma imagem ampliada de objetos que estavam próximos.

Em vista disso, ela afirmou CORRETAMENTE que:

a) as lentes dos óculos de Gustavo seriam mais finas nas bordas e espessas no meio.

b) os óculos de Gustavo jamais forneceriam uma imagem invertida de um objeto.

c) as lentes dos óculos de Gustavo seriam divergentes.

d) Gustavo é míope.

e) as lentes dos óculos de Gustavo seriam grossas nas bordas e finas no meio.

5) Um objeto de 10 cm de altura está posicionado a 7 cm de uma lente convergente de borda fina, de distância focal f = 5 cm. Determine a posição e a altura da imagem, respectivamente.

a) 17,5 cm e 25 cm.

b) 2,9 cm e -4,1 cm.

c) 2,9 cm e 4,1 cm.

d) 2 cm e -0,3 cm.

e) 17,5 cm e -25 cm.