Recuperação: interações gravitacionais.

  Recomendações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 06/10.

Olá pessoal! Que todos estejam bem.

Vamos revisar o que aprendemos sobre gravitação.

* Leis de Kepler.

Quando o ser humano iniciou a agricultura, ele necessitou de uma referência para identificar as épocas de plantio e colheita.

Ao observar o céu, os nossos ancestrais perceberam que alguns astros descrevem um movimento regular, o que propiciou a eles obter uma noção de tempo e de épocas do ano.

Primeiramente, foi concluído que o Sol e os demais planetas observados giravam em torno da Terra. Mas este modelo, chamado de Modelo Geocêntrico, apresentava diversas falhas, que incentivaram o estudo deste sistema por milhares de anos.

Por volta do século XVI, Nicolau Copérnico (1473-1543) apresentou um modelo Heliocêntrico, em que o Sol estava no centro do universo, e os planetas descreviam órbitas circulares ao seu redor.

No século XVII, Johanes Kepler (1571-1630) enunciou as leis que regem o movimento planetário, utilizando anotações do astrônomo Tycho Brahe (1546-1601).

Kepler formulou três leis que ficaram conhecidas como Leis de Kepler.

1ª Lei de Kepler - Lei das Órbitas

Os planetas descrevem órbitas elipticas em torno do Sol, que ocupa um dos focos da elipse.

2ª Lei de Kepler - Lei das Áreas

O segmento que une o sol a um planeta descreve áreas iguais em intervalos de tempo iguais.

3ª Lei de Kepler - Lei dos Períodos

O quociente dos quadrados dos períodos e o cubo de suas distâncias médias do sol é igual a uma constante k, igual a todos os planetas.

Tendo em vista que o movimento de translação de um planeta é equivalente ao tempo que este demora para percorrer uma volta em torno do Sol, é fácil concluirmos que, quanto mais longe o planeta estiver do Sol, mais longo será seu período de translação e, em consequência disso, maior será o "seu ano".

* Unidades astronômicas.

No estudo de astronomia muitas vezes as unidades do Sistema Internacional (SI) são ineficientes pois as distâncias que devem ser expressas são muito grandes.

Por exemplo: A distância da Terra até Marte é de cerca de 75 milhões de quilômetros, que no SI é expresso por 75 000 000 000 metros.

Devido à necessidade de unidades mais eficientes são utilizadas: Unidade Astronômica (UA), Anos-luz (AL) e Parsec (Pc).

Unidade Astronômica (UA)

É a distância média entre a Terra e o Sol. É empregada principalmente para descrever órbitas e distâncias dentro do Sistema Solar.

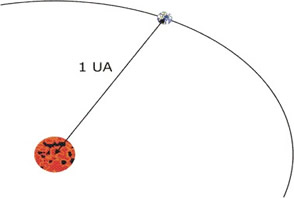
O tamanho médio da órbita dos planetas do Sistema Solar, ou seja, sua distância ao Sol é:

Planeta	Distância ao Sol (UA)
Mercúrio	0,39
Vênus	0,72
Terra	1,00
Marte	1,52
Júpter	5,20
Saturno	9,53
Urano	19,10
Netuno	30,00

Ano-Luz (al)

É a distância percorrida pela luz, no vácuo, no tempo de 1 ano terrestre.

Sendo a velocidade da luz c = 299 792,458 km/s, temos que:

1 al = 9 460 536 207 068 016 m = 63241,07710 UA

A estrela mais próxima do Sol é chamada Próxima Centauri, localizada na constelação de Centauro. A sua distância ao Sol é de 4,22 al

Parsec (Pc)

É a distância na qual 1 UA é representada por 1'' (1 segundo de arco), em uma medição por paralaxe.

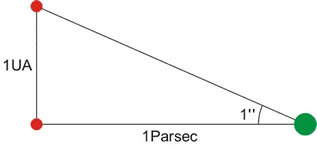
Esta unidade é usada para distância muito grandes, como a distância entre estrelas, entre galáxias ou de objetos muito distantes, como quasares.

Força gravitacional

Ao estudar o movimento da Lua, Newton concluiu que a força que faz com que ela esteja constantemente em órbita é do mesmo tipo que a força que a Terra exerce sobre um corpo em suas proximidades. A partir daí criou a Lei da Gravitação Universal.

Lei da Gravitação Universal de Newton:

"Dois corpos atraem-se com força proporcional às suas massas e inversamente proporcional ao quadrado da distância que separa seus centros de gravidade."

Onde:

F=Força de atração gravitacional entre os dois corpos

G=Constante de gravitação universal

M e m = massa dos corpos

d=distância entre os centros de gravidade dos corpos.

Nas proximidades da Terra a aceleração da gravidade varia, mas em toda a Litosfera (camada em que há vida) esta pode ser considerada constante, seus valores para algumas altitudes determinadas são:

Altitude (km)	Aceleração da Gravidade (m/s²)	Exemplo de altitude
0	9,83	nível do mar
8,8	9,80	cume do Monte Everest
36,6	9,71	maior altura atingida por balão tripulado
400	8,70	órbita de um ônibus espacial
35700	0,225	satélite de comunicação

A gravitação universal é uma força fundamental de atração que age entre todos os objetos, de acordo com a quantidade de matéria de que são constituídos (massa).

Confira a seguir uma lista de fórmulas sobre este conteúdo.

Força gravitacional
Força Gravitacional
Constante de gravitação universal
Leis de Kepler
1ª Lei de Kepler - Lei das Órbitas		"Os planetas descrevem órbitas elípticas em torno do Sol, que ocupa um dos focos da elipse."
2ª Lei de Kepler - Lei das Áreas		"O segmento que une o sol a um planeta descreve áreas iguais em intervalos de tempo iguais."
3ª Lei de Kepler - Lei dos Períodos

Um dos temas que proporcionou muitos debates ao longo da história foi a dinâmica do Sistema Solar. O interesse em compreender os movimentos dos corpos celestes gerou muitas observações, pesquisas e teorias religiosas e científicas sobre esse fenômeno.

Por volta de 350 a.C., na Grécia antiga, Aristóteles desenvolveu uma teoria que defendia a ideia de que a Terra era o centro do universo e nove esferas ficavam girando em torno dela. Posteriormente, no século II d.C., o matemático e astrônomo Claudio Ptolomeu reforçou esse pensamento e elaborou a teoria Geocêntrica, também chamada de sistema ptolomaico.

Sistematização do modelo Geocêntrico

Segundo essa teoria, a Terra está no centro do Sistema Solar, e os demais astros orbitam ao redor dela ao longo de um círculo (epiciclo). Conforme o geocentrismo, cada astro se movimenta com velocidade distinta, cuja ordem de proximidade da Terra é a seguinte: Lua, Mercúrio, Vênus, Sol, Marte, Júpiter e Saturno. Esse modelo de Sistema Solar foi defendido pela Igreja Católica durante mais de 1.400 anos, visto que apresentava aspectos de passagens bíblicas.

A teoria heliocêntrica já vinha sendo desenvolvida durante o século III a.C., através de observações do astrônomo grego Aristarco de Samos. No entanto, somente no século XVI d.C. foi que Nicolau Copérnico sistematizou uma teoria que contrapunha o modelo geocêntrico, sendo denominado heliocentrismo.

Nicolau Copérnico

Nicolau Copérnico (1473 – 1543), considerado o fundador da astronomia moderna, nasceu na Polônia e desenvolveu conhecimentos nos campos da matemática, geografia e astronomia. Sua teoria heliocêntrica afirmava que a Terra e os demais planetas se moviam ao redor de um ponto vizinho ao Sol, sendo, este, o verdadeiro centro do Sistema Solar. A alternância entre dias e noites é uma consequência do movimento que a Terra realiza sobre seu próprio eixo, denominado movimento de rotação.

Rapidamente, a Igreja Católica se opôs à teoria heliocêntrica, e Copérnico só autorizou a divulgação de seus dados matemáticos que comprovavam a teoria após sua morte, pois temia ser condenado por heresia pela Igreja Católica.

Posteriormente, Galileu Galilei, durante o século XVII, reforçou a teoria heliocêntrica através de observações com lunetas holandesas. Como consequência de seu “atrevimento”, Galileu foi julgado pelo tribunal da Inquisição, tendo como opção negar sua teoria ou ser queimado na fogueira da Inquisição. Sem muitas alternativas, sua teoria foi negada.

Porém, o heliocentrismo foi sendo aperfeiçoado por cientistas e astrônomos como Michael Maestlin, Johannes Kepler e Isaac Newton, e, atualmente, é a teoria mais aceita pela comunidade científica. A Igreja Católica, por sua vez, só aceitou esse modelo de Sistema Solar em 1922.

Por Wagner de Cerqueira e Francisco
Graduado em Geografia

Exemplos

1) Determine por meio da lei dos períodos proposta por Kepler o período de revolução de um planeta que está a 9 UA do Sol.

Dado: UA: unidade astronômica.

Resolução:

Aplicando a Terceira Lei de Kepler, temos:

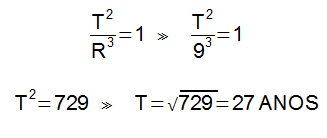
2) Quando o raio médio da órbita de um planeta está em unidade astronômica (UA), e o período de revolução está em anos terrestres, o resultado da lei dos períodos aplicada a qualquer planeta deve tender a 1. Qual deverá ser o raio médio da órbita de um planeta qualquer do sistema solar, em UA, que possui período de translação de oito anos?

Resolução:

Aplicando a Terceira Lei de Kepler, temos:

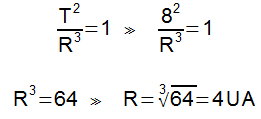
3) A intensidade da força gravitacional com que a Terra atrai a Lua é F. Se fossem duplicadas a massa da Terra e da Lua e se a distância que as separa fosse reduzida à metade, a nova força seria:

a) 16F

b) 8F

c) 4F

d) 2F

e) F

Resolução:

F = G . M_T . m_l
                r²

d = r/2, M = 2M_T e m=2m_l

F' = G . 2M_T . 2M_l
                  (r/2)²

F' = 4 . G . M_T . M_l
                      r²/4

F' = 16 G . M_T . m_l
                      r²

F' = 16F – Alternativa A

4) Calcule a força de atração gravitacional entre duas massas de 500 kg distantes 5 m uma da outra.

Resolução:

Fg = G . M . m
              r²

Fg = 6,67 . 10^-11 . 500 . 500
                      5²

Fg = 6,67 . 10^-7 N

5) A força da atração gravitacional entre dois corpos celestes é proporcional ao inverso do quadrado da distância entre os dois corpos. Assim, quando a distância entre um cometa e o Sol diminui da metade, a força de atração exercida pelo Sol sobre o cometa:

a) diminui da metade;

b) é multiplicada por 2;

c) é dividida por 4;

d) é multiplicada por 4;

e) permanece constante.

Resolução:

A força gravitacional entre o Sol e o cometa é dada pela expressão:

F = G . M_S . M_c
          r²

Quando r diminui pela metade, passa a ser r/2, e a força gravitacional pode ser reescrita como:

F' = G . M_S . M_c
          (r/2)²

F' = G . M_S . M_c
         r²/4

F' = 4 G . M_S . M_c
           r²

F' = 4F

O resultado obtido mostra que a força F fica multiplicada por 4 – Alternativa d.

Assistam a vídeo aula com o Professor Douglas Gomes através do link:

https://youtu.be/INh4C6SITuA (vídeo disponível no YouTube.

Agora faça os exercícios.

Exercícios.

1) Determine por meio da lei dos períodos proposta por Kepler o período de revolução de um planeta que está a 4 UA do Sol.

Dado: UA: unidade astronômica.

a) 2 anos

b) 4anos

c) 6 anos

d) 8 anos

e) 10 anos

2) Qual deverá ser o raio médio da órbita de um planeta qualquer do sistema solar, em UA, que possui período de translação de 64 anos?

a) 16 UA

b) 12 UA

c) 10 UA

d) 8 UA

e) 6 UA

3) Determine a força de atração entre o Sol e a Terra, sabendo que a massa da Terra é 6.10 ²⁴ kg, a massa do Sol é 2. 10³⁰ kg e a distância entre os dois astros é de 1,5.10⁸ km.

Dado: 1 km = 10³ m

a) 2,1 . 10 ²² N

b) 4,58 . 10 ²² N

c) 1,51 . 10²² N

d) 2,52 . 10 ²² N

e) 3,52 . 10²² N

4) Marque a alternativa correta a respeito do modelo astronômico proposto por Cláudio Ptolomeu.

a) O modelo ptolomaico propunha que o Sol girava ao redor da Terra e todos os outros planetas giravam ao redor do Sol.

b) O sistema planetário proposto por Ptolomeu trazia a ideia de que a Terra era o centro do Universo e os demais astros giravam ao seu redor.

c) Nicolau Copérnico no século XVI propôs que a Terra era o centro do sistema planetário, proposta que era contrária à de Ptolomeu.

d) A proposta de Ptolomeu era a de um universo simples, por isso, o Sol deveria ser o centro e os demais planetas girariam ao seu redor.

e) O modelo planetário proposto por Ptolomeu não foi aceito por muito tempo porque confrontava as ideias da Igreja.

5) Em relação à unidade astronômica (UA), assinale a alternativa correta.

a) Unidade astronômica é o nome dado à distância percorrida pela luz no vácuo durante o intervalo de tempo de um ano.

b) Unidade astronômica é definida como a distância média entre a Terra e Marte.

c)  Unidade astronômica é definida como a distância média entre a Terra e o Sol.

d) Unidade astronômica é o nome da distância média entre a Terra e a Lua.

e) No vácuo, a luz demora cerca de 1 segundo para percorrer a distância de 1 unidade astronômica.