Óptica geométrica: refração da luz.

  Recomendações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 06/10.

Olá pessoal! Que todos estejam bem.

Nessa semana vamos estudar a refração da luz. 

Refração é a mudança na velocidade de propagação da luz em um determinado meio. Por exemplo, quando a luz passa do ar para água. Como o ar é um meio diferente da água, a luz se propaga com velocidades diferentes nesses meios. Isso é o que se chama de refração da luz.

A refração da luz é um fenômeno óptico que ocorre quando a luz sofre mudança do meio de propagação, ou seja, do meio de incidência para o meio de refração, onde há variação de velocidade da propagação. Lembre-se que a luz é uma forma de onda que se propaga em determinada velocidade e essa velocidade dependerá do meio no qual ela se propaga.

Dessa maneira, considera-se a velocidade da luz no ar, diferente da água, de modo que quando passa de um meio para o outro, seja um copo de vidro com água, ocorre a refração, ou o desvio do feixe de luz.

Nesse processo, ocorrerá a diminuição da velocidade da luz e do comprimento da onda, entretanto a frequência (constante de proporcionalidade) não será alterada. Por isso, quando colocamos um objeto num copo com água, ou quando observamos uma piscina estando fora dela, temos a ilusão de que o objeto está quebrado, no caso do copo, e a piscina possuir menor profundidade.

Incidência da luz

No fenômeno da refração, ocorre a alteração da velocidade de propagação da luz por meio de um desvio da direção original, ou seja, a luz sofre um desvio angular em relação à reta normal, de modo que passa de um meio transparente para outro transparente diferente.

Assim, se a incidência da luz no meio for normal, ou seja, apresenta o ângulo de incidência igual a zero, a luz não sofrerá desvio e, portanto, seu ângulo refratado será nulo. Por outro lado, quando a incidência da luz provoca um desvio oblíquo, o raio luminoso se aproximará mais da reta normal, levando ao desvio na trajetória luminosa, ou seja, o fenômeno da refração.

Nesta mudança de meios a frequência da onda luminosa não é alterada, embora sua velocidade e o seu comprimento de onda sejam.

Com a alteração da velocidade de propagação ocorre um desvio da direção original.

Para se entender melhor este fenômeno, imagine um raio de luz que passa de um meio para outro de superfície plana, conforme mostra a figura abaixo:

Onde:

• Raio 1 é o raio incidente, com velocidade e comprimento de onda característico;
• Raio 2 é o raio refratado, com velocidade e comprimento de onda característico;
• A reta tracejada é a linha normal à superfície;
• O ângulo formado entre o raio 1 e a reta normal é o ângulo de incidência (Θ1);
• O ângulo formado entre o raio 2 e a reta normal é o ângulo de refração (Θ2);
• A fronteira entre os dois meios é um dioptro plano.

Conhecendo os elementos de uma refração podemos entender o fenômeno através das duas leis que o regem.

1ª Lei da Refração

A 1ª lei da refração diz que o raio incidente (raio 1), o raio refratado (raio 2) e a reta normal ao ponto de incidência (reta tracejada) estão contidos no mesmo plano, que no caso do desenho acima é o plano da tela.

2ª Lei da Refração - Lei de Snell

A 2ª lei da refração é utilizada para calcular o desvio dos raios de luz ao mudarem de meio, e é expressa por:

No entanto, sabemos que:

Além de que:

Ao agruparmos estas informações, chegamos a uma forma completa da Lei de Snell:

Onde:

senΘ1 = seno do ângulo de incidência.

senΘ2 = seno do ângulo de refração.

V1 = velocidade da luz no meio 1.

V2 = velocidade da luz no meio 2.

λ1 = comprimento de onda da luz no meio 1.

λ2 = comprimento de onda da luz no meio 2.

n1 = índice de refração do meio 1.

n2 = índice de refração do meio 2.

Observação.

Quanto menor o índice de refração (n), maior é a velocidade da luz no meio.

Dioptro

É todo o sistema formado por dois meios homogêneos e transparentes.

Quando esta separação acontece em um meio plano, chamamos então, dioptro plano.

A figura abaixo representa um dioptro plano, na separação entre a água e o ar, que são dois meios homogêneos e transparentes.

Formação de imagens através de um dioptro

Considere um pescador que vê um peixe em um lago. O peixe encontra-se a uma profundidade H da superfície da água. O pescador o vê a uma profundidade h. Conforme mostra a figura abaixo:

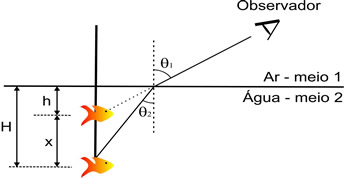
A fórmula que determina estas distância é:

Como:

senî/senr = hi/ho → n2/n1 = hi/ho → hi/ho = n vai/n vem

Observação:

H = ho: profundidade do objeto

h = hi: profundidade da imagem.

n vai: índice de refração do meio para o qual a luz vai (em relação ao observador)

n vem: índice de refração do meio para o qual a luz vai (em relação ao obsdervador)

Ângulo limite e reflexão total.

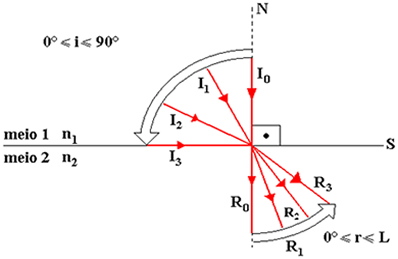
Supondo-se dois meios homogêneos e transparentes separados por uma superfície plana chamada S, na qual o meio 1 é menos refringente que o meio 2, ou seja, n1 > n2, e considerando-se um raio de luz monocromática passando do meio 1 para o meio 2, é possível variar o ângulo de incidência de 0° até o máximo 90° que haverá ocorrência da refração. Na figura acima, estão indicados os raios incidentes I0 (i = 0°), I1, I2, e I3 (i = 90°) e os seus respectivos raios refratados R0 (r = 0), R1, R2 e R3 (r = L).

Como o ângulo de incidência máximo é i = 90°, o correspondente ângulo de refração máximo r = L é denominado ângulo limite.

Para um par de meios, o ângulo limite é obtido através da Lei de Snell-Descartes aplicado aos raios I3 (incidência máxima) e R3 (refração máxima). Assim, temos:

sen i .n1=sen r .n2

sen 90° .n1=sen L .n2

Como sen 90° = 1, temos:

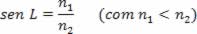
Pela Lei da Reversibilidade dos Raios Luminosos, é possível inverter o sentido de percurso dos raios da figura anterior. Desse modo, os raios incidentes estarão no meio mais refringente; e os raios refratados, no menos refringente; conforme vemos na figura abaixo.

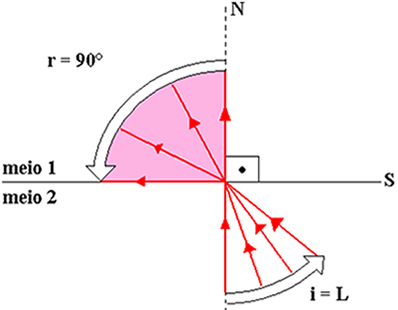
Como os raios incidentes estão no meio 2, é possível ter ângulos de incidência maiores que o ângulo limite L. Esses raios não mais se refratam, ocasionando sua reflexão total, conforme a figura abaixo.

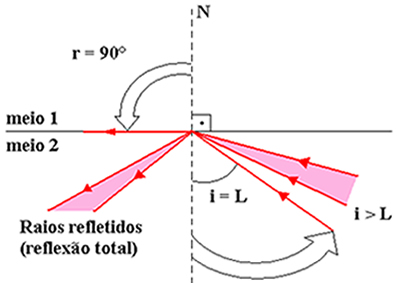
A superfície S, para esses raios, funciona como um perfeito espelho, com a superfície refletora voltada para o meio 2. Obviamente, os raios obedecem às Leis da Reflexão dos Espelhos.

Concluindo, existem duas condições para a ocorrência da reflexão total:

1)      A luz incidente deve estar se propagando do meio mais refringente para o meio menos refringente.

2)     O ângulo de incidência deve ser maior que o ângulo limite (i > L).

Na figura acima temos os raios incidentes e os respectivos raios refratados

Como o ângulo de incidência máximo mede i = 90°, o correspondenteângulo de refração máximo r = L é denominado ângulo limite.

sen L = n menor/n maior

Resumo.

Definições

• Ângulo de incidência:é o ângulo entre o raio incidente e a reta normal;

• Ângulo de refração:é o ângulo entre a normal e o raio refratado.

 

 

Índice de refração

Ao mudar de um meio para o outro, existe também uma mudança de velocidade. Podemos medir essa diferença através do índice de refração.

Sejam:

• : índice de refração do meio;

• : a velocidade da luz no vácuo (m/s);

• : a velocidade da luz no meio.

Temos que:

 

Leis da refração

• 1ª Lei: Raio incidente, raio refratado e a reto normal são coplanares;

• 2ª Lei (Lei de Snell-Descartes): Sejam,índices de refração respectivamente do meio 1 e do meio 2. Temos que:

n1 . sen i = n2 . sen r

Ângulo Limite e Reflexão Total

Reflexão total

Seja um cenário onde a luz parte de um meio com índice de refração maior para um meio com índice menor.

Ao aumentar o ângulo de incidência, o raio de refração vai se aproximando do limite entre os dois meios. Quando o ângulo de refraçãofor 90º, o raio refratado coincidirá com esse limite. Nesse caso em especifico, oângulo de incidênciaé chamado de ângulo limite e temos que:

Todo raio cujo ângulo de incidência for maior que o ângulo limite, será refletido.

Dioptro Plano

Seja um cenário onde temos dois meios diferentes, homogêneos e transparentes.

Quando um observador vê um objeto que está no outro meio, existe uma distorção em relação à verdadeira localização desse objeto.

Sejam:

• : distância entre a imagem observada do objeto e o limite entre os meios;

• : distância entre o objeto real e o limite entre os meios;

• : índice de refração do meio onde o raio incide;

• : índice de refração do meio onde o raio refrata.

Temos que:

 Exemplos.

Ao aluno cabe saber os valores dos senos, cossenos e tangente dos ângulos notáveis ( 30°, 45°, 60° ).

           

1) Uma fonte monocromática F, imersa em um líquido de índice de refração nlíquido = 2, emite luz que se propaga do líquido para o ar, sendo índice de refração do ar nar = 1. Ângulo limite desse par de meios, vale:

Resolução:

sen L = n menor/n maior

sen L = 1/2     (o ângulo cujo seno é 1/2 é 30°)

L = 30°

2) Em relação a superfície da piscina, qual é a altura aparente, x, que uma pessoa submersa vê um avião que voa a 1500 metros de altura?

Dados: nar=1 e nágua=4/3

Resolução:

O observador está dentro da água da piscina. Assim, temos que a luz sai do avião e vai para o observador.

hi/ho = n vai/ n vem

hi/1500 = (4/3)/1

1 . hi = 1500 . 4/3

hi = 6000/3

hi = 2000 m

Resposta: Atura aparente do avião em relação à superfície da água na piscina é 2000 m.

3) Uma onda eletromagnética se propaga no vácuo e incide sobre uma superfície de um cristal fazendo um ângulo de1=60° com a direção normal a superfície. Considerando a velocidade de propagação da onda no vácuo como c=3 x 108 m/s e sabendo que a onda refratada faz um ângulo de2= 30° com a direção normal, podemos dizer que a velocidade de propagação da onda no cristal em m/s é:

a) 1 . 10⁸

b) ⎷2 . 10⁸

c) ⎷3 . 10⁸

d) 2 . 10⁸

e) ⎷5 . 10⁸

Resolução:

Pela lei de Snell, temos:

sen i/sen r = vi/vr

sen 60°/sen 30° = 3 . 10⁸/vr

(⎷3/2)/(1/2) = 3 . 10⁸/vr

(⎷3/2) . 2 = 3 . 10⁸/vr

⎷3 = 3 . 10⁸/vr

vr . ⎷3 = 3 . 10⁸

vr = 3 . 10⁸/⎷3   ( fazendo a racionalização )

vr = ⎷3 . 10⁸ m/s

Resposta: C

4) Uma onda luminosa se propaga em um meio cujo índice de refração é 1,5. Considerando a velocidade da luz no vácuo igual a 3,0x108 m/s, a velocidade de propagação desta onda luminosa no meio, em m/s, é igual a:

a) 0,5 . 10⁸

b) 1 . 10⁸

c) 1,5 . 10⁸

d) 2 . 10⁸

e) 2,5 . 10⁸

Resolução:

O indice de refração no vácuo é sempre igual a 1.

Pela lei deSnell, temos:

n1/n2 = V2/V1

1,5/1 = 3 . 10⁸/V1

1,5 . V1 = 3 . 10⁸

V1 = 3 . 10⁸/1,5

V1 = 2 . 10⁸ m/s

Resposta: D

Assistam a vídeo aula com o Professor Boaro, pelo link: https://youtu.be/gvUfJXIHybIY

Agora façam os exercícios que seguem.

Exercícios.

1) Será que uma miragem ajudou a afundar o Titanic? O fenômeno ótico conhecido como Fata Morgana pode fazer com que uma falsa parede de água apareça sobre o horizonte molhado. Quando as condições são favoráveis, a luz refletida pela água fria pode ser desviada por uma camada incomum de ar quente acima, chegando até o observador, vinda de muitos ângulos diferentes. De acordo com estudos de pesquisadores da Universidade de San Diego, uma Fata Morgana pode ter obscurecido os icebergs da visão da tripulação que estava a bordo do Titanic. Dessa forma, a certa distância, o horizonte verdadeiro fica encoberto por uma névoa escurecida, que se parece muito com águas calmas no escuro.

Disponível em: http://apod.nasa.gov. Acesso em: 6 set. 2012 (adaptado).

O fenômeno ótico que, segundo os pesquisadores, provoca a Fata Morgana é a:

a) ressonância

b) reflexão

c) refração

d) difusão

e) difração

2) Quando olhamos uma piscina, estando em pé e do lado de fora da mesma, sempre temos a impressão de que ela tem uma profundidade diferente da que percebemos quando nela mergulhamos. Isso se deve ao fato de que o ar atmosférico e a água têm índices de refração absolutos diferentes. Se a profundidade real de uma piscina é 2,0m e os índices de refração absolutos do ar atmosférico e da água da piscina valem 1,0 e 1,3 respectivamente, é correto dizer que um observador em pé, fora da piscina, verá que a sua profundidade será, aproximadamente, em metros:

a) 2,6 m

b) 2,2 m

c) 2 m

d) 1,5 m

e) 1 m

3) Alguns povos indígenas ainda preservam suas tradições realizando a pesca com lanças, demonstrando uma notável habilidade. Para fisgar um peixe em um lago com águas tranquilas o índio deve mirar abaixo da posição em que enxerga o peixe.

Ele deve proceder dessa forma porque os raios de luz:

a) refletidos pelo peixe não descrevem uma trajetória retilínea dentro da água.

b) emitidos pelos olhos do índio desviam quando passam do ar para a água.

c) espalhados pelo peixe são refletidos pela superfície da água.

d) emitidos pelos olhos do índio são espalhados na superfície da água.

e) refletidos pelo peixe desviam sua trajetória quando passam da água para o ar.

4) Antes do seu emprego nas comunicações, as fibras óticas já vinham sendo usadas para a iluminação e inspeção das cavidades do corpo humano, o que possibilitou o desenvolvimento de técnicas diagnósticas como a endoscopia. O fenômeno físico que permite guiar a luz, através de um feixe de fibras flexíveis, por um caminho curvo é a reflexão interna total. Para que esse fenômeno ocorra,

I. a luz deve incidir a partir de um meio de índice de refração mais alto sobre a interface com um meio de índice de refração mais baixo.
II. o ângulo de incidência da luz sobre a interface de separação entre dois meios deve ser tal que o ângulo de refração seja de, no mínimo, 90º
III. a interface de separação entre os meios interno e externo deve ser revestida com um filme refletor.

Está(ão) correta(s):

a) apenas I.

b) I e II.

c) apenas II.

d) II e III.

e) I, II e III.

5)  Uma onda eletromagnética se propaga no vácuo e incide sobre uma superfície de um cristal fazendo um ângulo de θ1= 60° com a direção normal a superfície. Considerando a velocidade de propagação da onda no vácuo como c=3 x 108 m/s e sabendo que a onda refratada faz um ângulo de θ2= 45° com a direção normal, podemos dizer que a velocidade de propagação da onda no cristal em m/s é:

a) ⎷6 . 10⁸ m/s

b) ⎷3 . 10⁸ m/s

c) ⎷ 2 . 10⁸ m/s

d) ⎷5 . 10⁸ m/s

e) 3⎷6 . 10⁸ m/s