Leis de Kepler.

Orientações aos alunos:
* Leiam com atenção e observem os exemplos.
* Assistam às aulas pelo CMSP, TV, Plataforma Stoodi e façam pesquisas em livros didáticos ou pela internet.
* Identifiquem as atividades com a data de postagem, nome, turma, série e nº de chamada (se possível).
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 08/09.
Olá pessoal! Que todos estejam bem.
Vamos continuar  o nosso estudo sobre o Universo. Nessa semana vamos estudar as leis de Kepler.
No estudo de gravitação universal, as leis de Kepler são fundamentais.

As leis de Kepler.

As Leis de Kepler são três leis, propostas no século XVII, pelo astrônomo e matemático alemão Johannes Kepler (1571-1630), na obra Astronomia Nova (1609).

Elas descrevem os movimentos dos planetas, seguindo modelos heliocêntricos, ou seja, o Sol no centro do sistema solar.

Primeira Lei de Kepler: lei das órbitas.

A 1ª Lei descreve as órbitas dos planetas. Kepler propôs que os planetas giram em torno do Sol, em uma órbita elíptica, com o Sol em um dos focos.

Nesta Lei, Kepler corrige o modelo proposto por Copérnico que descrevia como circular o movimento orbital dos planetas.

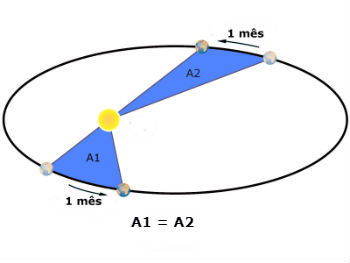
Segunda Lei de Kepler: lei das áreas.

A 2ª lei de Kepler assegura que o segmento (raio vetor) que une o sol a um planeta varre áreas iguais em intervalos de tempo iguais.

Uma consequência deste fato é que a velocidade do planeta ao longo da sua trajetória orbital é diferente.

Sendo maior quando o planeta se encontra mais próximo do seu periélio (menor distância entre o planeta e o Sol) e menor quando o planeta se encontra próximo do seu afélio (maior distância do planeta ao Sol).

Terceira Lei de Kepler: lei dos períodos.

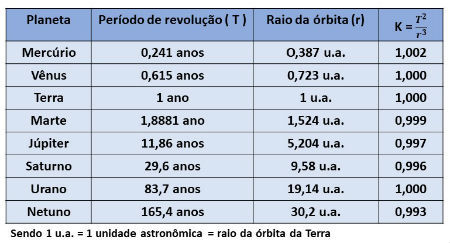
A 3ª lei de Kepler indica que o quadrado do período de revolução de cada planeta é proporcional ao cubo do raio médio de sua órbita.

Por isso, quanto mais distante o planeta estiver do sol, mais tempo levará para completar a translação.
Matematicamente, a terceira Lei de Kepler é descrita da seguinte maneira:

Onde:

T: corresponde ao tempo de translação do planeta
r: o raio médio da órbita do planeta
K: valor constante, ou seja, apresenta o mesmo valor para todos os corpos que orbitam ao redor do Sol. A constante K depende do valor da massa do Sol.

Para qualquer planeta da galáxia, vale a lei dos períodos.

Portanto, a razão entre os quadrados dos períodos de translação dos planetas e os cubos dos respectivos raios médios das órbitas será sempre constante, conforme apresentado na tabela abaixo:

Leis de Kepler e a Gravitação Universal

As Leis de Kepler descrevem o movimento dos planetas, sem se preocupar com as suas causas.

Isaac Newton ao estudar essas Leis, identificou que a velocidade dos planetas ao longo da trajetória é variável em valor e direção.

Para explicar essa variação, ele identificou que existiam forças atuando nos planetas e no Sol.

Deduziu que essas forças de atração dependem da massa dos corpos envolvidos e das suas distâncias.

Chamada de Lei de Gravitação Universal, sua expressão matemática é:

Sendo,

F: força gravitacional
G: constante de gravitação universal, sendo igual a 6,67.10^-11 N.m²/kg²
M: massa do Sol
m: massa do planeta

R: distância de centro a centro dos planetas.

Assista ao vídeo pelo link abaixo:

https://www.youtube.com/watch?v=6jXN_1Xt20M#action=share

Exemplos.

1) Calcule aproximadamente o período de rotação de um satélite artificial da Terra cujo raio da órbita é 2 vezes menor que o raio da órbita da Lua. Considere que o período de rotação da Lua ao redor da Terra é igual a 28 dias.
Resolução:
Pela 3ª lei de Kepler, temos:

Tl² = Ts²

Rl³    Rs³

28² = Ts²             

Rl³    (Rl/2)³

784 = Ts²                ( Multiplica em cruz )

Rl³     Rl³/8

Ts² . Rl³ = 784 . Rl³/8

Ts² = 784/8

Ts² = 98

Ts = ⎷98

Ts = 9,899

Resposta: O período de rotação do satélite é de aproximadamente 10 dias.

2) Certo planeta A, que orbita em torno do Sol, tem período orbital de 1 ano. Se um planeta B, tem raio orbital 3 vezes maior, qual será o tempo necessário para que esse planeta complete uma volta em torno do Sol.

Resolução:

Para resolvermos o exercício, usaremos a Terceira Lei de Kepler, para tanto, basta identificar que o raio orbital do planeta B é igual a 3R_a, fazendo isso, temos que fazer o seguinte cálculo:

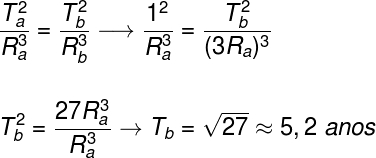
De acordo com o cálculo feito, o período orbital do planeta B é igual a 5,2 anos.

3) A intensidade da força gravitacional com que a Terra atrai a Lua é F. Se fossem duplicadas a massa da Terra e da Lua e se a distância que as separa fosse reduzida à metade, a nova força seria:

a) 16F

b) 8F

c) 4F

d) 2F

e) F

Resolução: 

F = G . M_T . m_l
                r²

d = r/2, M = 2M_T e m=2m_l

F' = G . 2M_T . 2M_l
                  (r/2)²

F' = 4 . G . M_T . M_l
                      r²/4

F' = 16 G . M_T . m_l
                      r²

F' = 16F 

Alternativa A

4) Determine a força de atração entre o Sol e a Terra em termos de 10²² N sabendo que a massa da Terra é 6.10 ²⁴ kg, a massa do Sol é 2. 10³⁰ kg e a distância entre os dois astros é de 1,5.10⁸ km.

Dado: 1 km = 10³ m

Resolução:

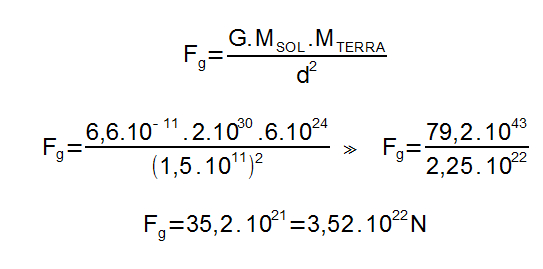
Agora faça os exercícios.

Exercícios.

1) O modelo de universo proposto por Kepler, apesar de Heliocêntrico, tinha disparidades com o modelo de Copérnico. Marque a alternativa que contém tais disparidades.

a) Copérnico acreditava que os planetas giravam em torno do Sol em movimentos uniformes. A 3ª lei de Kepler mostra que esses movimentos são variados.

b) No modelo de Copérnico as trajetórias dos planetas eram elípticas, enquanto no de Kepler as trajetórias eram circulares. Como sabemos hoje, as trajetórias dos planetas ao redor do sol são elípticas.

c) No modelo de Copérnico as trajetórias dos planetas eram circulares, enquanto no de Kepler as trajetórias eram elípticas. Como sabemos hoje, as trajetórias dos planetas ao redor do sol são elípticas.

d) Copérnico acreditava também, de forma errada, que o movimento no céu era circular e uniforme. A 2ª lei de Kepler nos mostra que o movimento dos planetas ao redor do centro da galáxia é variado.

e) N.D.A

2) O astrônomo alemão J. Kepler (1571-1630), adepto do sistema heliocêntrico, desenvolveu um trabalho de grande vulto, aperfeiçoando as ideias de Copérnico. Em consequência, ele conseguiu estabelecer três leis sobre o movimento dos planetas, que permitiram um grande avanço no estudo da astronomia. Um estudante ao ter tomado conhecimento das leis de Kepler concluiu, segundo as proposições a seguir, que:

I. Para a primeira lei de Kepler (lei das órbitas), o verão ocorre quando a Terra está mais próxima do Sol, e o inverno, quando ela está mais afastada.

II. Para a segunda lei de Kepler (lei das áreas), a velocidade de um planeta X, em sua órbita, diminui à medida que ele se afasta do Sol.

III. Para a terceira lei de Kepler (lei dos períodos), o período de rotação de um planeta em torno de seu eixo, é tanto maior quanto maior for seu período de revolução.

Com base na análise feita, assinale a alternativa correta:

a) apenas as proposições II e III são verdadeiras

b) apenas as proposições I e II são verdadeiras

c) apenas a proposição I é verdadeira

d) apenas a proposição II é verdadeira

e) todas as proposições são verdadeiras

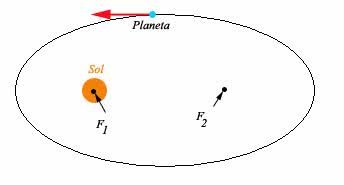
3) A figura a seguir, representa a órbita de um planeta ao redor do Sol:

Os arcos de órbita MN e OP são percorridos em intervalos de tempo iguais, qual a relação entre as áreas A1 e A2?

a.

b.

c.

d.

e.

4) Considere o raio médio da órbita de Júpiter em tomo do Sol igual a 5 vezes o raio médio da órbita da Terra.

Segundo a 3a Lei de Kepler, o período de revolução de Júpiter em tomo do Sol é de aproximadamente

a.

5 anos.

b.

11 anos.

c.

25 anos.

d.

110 anos.

e.

125 anos.

5) A respeito da lei da gravitação universal, marque a alternativa verdadeira:

a) A equação da lei da gravitação universal prevê tanto uma força de atração como uma de repulsão.

b) Se a distância entre dois objetos for triplicada, a força gravitacional entre eles será seis vezes menor.

c) Se as massas dos planetas do sistema solar sofressem variações consideráveis, nada mudaria, pois a força gravitacional depende apenas da massa do Sol.

d) A força gravitacional é diretamente proporcional ao quadrado da distância que separa dois corpos.

e) A força de atração gravitacional é inversamente proporcional ao quadrado da distância que separa os dois corpos.