Lançamentos oblíquos.

 Recomendações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 29/09.

Olá pessoal! Que todos estejam bem.

Vamos continuar o nosso estudo sobre interações gravitacionais. Vamos estudar nessa semana os lançamentos oblíquos.

Para a resolução dos exercícios, devemos observar que:

1) O corpo terá movimento na vertical e na horizontal. Sendo que na vertical é M.U.V, pois há a aceleração da gravidade. A gravidade é negativa na subida do corpo e positiva na descida do corpo.

As equações são:

V = Vo + g . t

S = So + Vo.t + g/2.t²

V² = Vo² + 2 . g . ΔS

2) Quando o corpo atinge a altura máxima, temos V = 0. O corpo para de subir e começa a cair.

3) Na horizontal o movimento é uniforme, pois desconsiderando a resistência do ar, não há forças dissipativas. Valendo a equação S = So + v.t

4) Devemos decompor a velocidade nos eixos X e Y, sendo: Vx = V . cosθ e Vy = V . senθ

5) Desprezando a resistência do ar, os corpos caem com a mesma velocidade, independente de suas massas.

Lembrando que a queda livre ocorre próximo à superfície terrestre, no vácuo.

Lançamento Oblíquo

O lançamento oblíquo ou de projétil é um movimento realizado por um objeto que é lançado na diagonal.

Esse tipo de movimento realiza uma trajetória parabólica, unindo movimentos na vertical (sobe e desce) e na horizontal. Assim, o objeto arremessado forma um ângulo (θ) entre 0° e 90° em relação a horizontal.

Na direção vertical ele realiza um Movimento Uniformemente Variado (MUV). Já na posição horizontal, o Movimento Retilíneo Uniforme (MRU).

Nesse caso, o objeto é lançado com uma velocidade inicial (v0) e está sob a ação da força da gravidade (g).

Geralmente, a velocidade vertical é indicado por vY, enquanto a horizontal é vX. Isso porque quando ilustramos o lançamento oblíquo, utilizamos dois eixos (x e y) para indicar os dois movimentos realizados.

A posição inicial (s0) indica o local onde tem início o lançamento. Já a posição final (sf) indica o final do lançamento, ou seja, o local onde o objeto cessa o movimento parabólico.

Além disso, é importante notar que após lançado ele segue na direção vertical até atingir uma altura máxima e daí, tende a descer, também na vertical.

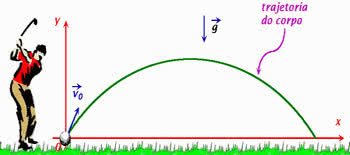
Como exemplos de lançamento oblíquo podemos citar: o chute de um futebolista, um atleta de salto à distância ou ainda, a trajetória realizada por uma bola de golfe.

Além do lançamento oblíquo, temos também:

• Lançamento Vertical: objeto lançado que realiza um movimento na vertical.
• Lançamento Horizontal: objeto lançado que realiza um movimento na horizontal.

Fórmulas

Para calcular o lançamento oblíquo no sentido vertical, utiliza-se a fórmula da Equação de Torricelli:

v2 = v02 + 2 . a . Δs

Onde,

v: velocidade final
v0: velocidade inicial
a: aceleração
ΔS: variação de deslocamento do corpo

Ela é utilizada para calcular a altura máxima atingida pelo objeto. Assim, a partir da equação de Torricelli podemos calcular a altura decorrente do ângulo formado:

H = v02 . sen2θ/2 . g

Onde:

H: altura máxima
v0: velocidade inicial
sen θ: ângulo realizado pelo objeto
g: aceleração da gravidade

Além disso, podemos calcular o lançamento oblíquo do movimento realizado na horizontal.

Importante notar que, nesse caso o corpo não sofre aceleração da gravidade. Assim, temos a equação horária do MRU:

S = S0 + V . t

Onde,

S: posição
S0: posição inicial
V: velocidade
t: tempo

A partir dela, podemos calcular o alcance horizontal do objeto:

A = v . cosθ . t

Onde,

A: alcance do objeto na horizontal
v: velocidade do objeto
cos θ: ângulo realizado pelo objeto
t: tempo

Posto que o objeto lançado retorna ao solo, o valor a ser considerado é o dobro do tempo de subida.

Assim, a fórmula que determina o alcance máximo do corpo é definido da seguinte maneira:

A = v2. sen2θ/g

O alcance será o máximo possível quando o ângulo de lançamento for igual a 45°. Como o ângulo é multiplicado por dois na equação do alcance, o seno calculado será o de 90°, que corresponde ao máximo valor de seno possível, assim o alcance será o máximo possível.

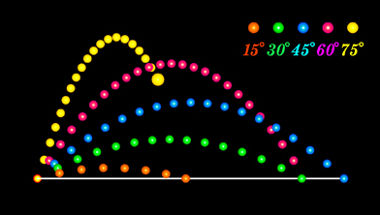
A imagem abaixo indica as possíveis trajetórias para lançamentos oblíquos executados sobre ângulos diversos. Observe que o maior alcance ocorre quando o ângulo de lançamento é igual a 45º.

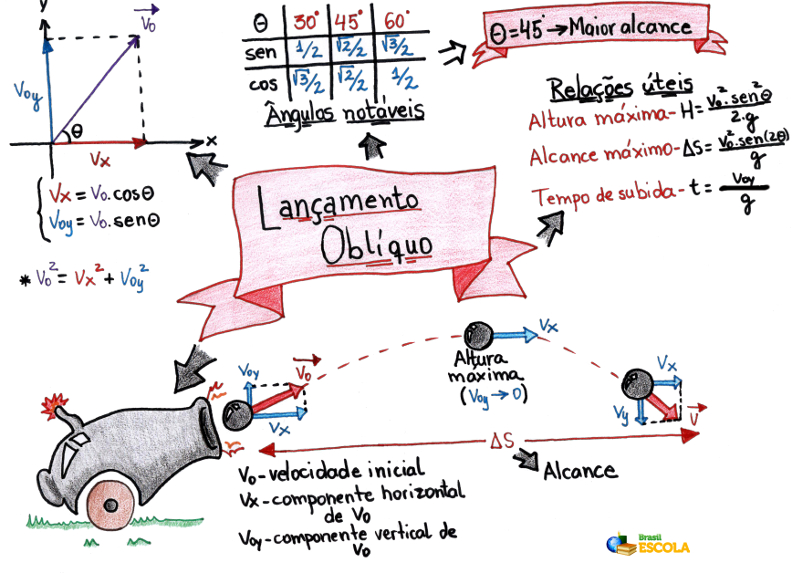
Mapa Mental: Lançamento Oblíquo

Exemplos.

1) Um canhão dispara uma bala com velocidade inicial igual a 500m/s (em módulo), a 45° com a horizontal. Desprezando o atrito e considerando g = 10m/s², determine o alcance máximo horizontal da bala.

Resolução:

A = v2. sen2θ/g

A = 500² . sen 2. 45/10

A = 250000 . sen 90/10

A = 250000 . 1/10

A = 250000 . 0,1

A = 25000 m

Resposta: A bala do canhão terá um alcance máximo de 25000m

2) Um projétil é lançado segundo um ângulo de 30° com a horizontal, com uma velocidade de 200m/s. Supondo a aceleração da gravidade igual a 10 m/s² e desprezando a resistência do ar, o intervalo de tempo entre as passagens do projétil pelos pontos de altura 480 m acima do ponto de lançamento, em segundos, é:

(DADOS: sen 30° = 0,50 e cos 30° = 0,87)

Resolução:

Pela função horária das posições do MUV, temos:

S = S_o + V_oy.t – g.t²/2
S-So = Voy.t – g.t²/2
480 = V.sen30.t – 10.t²/2
480 = 100.t – 5.t²
5.t² - 100.t + 480 = 0
t² - 20.t + 96 = 0

Como a equação é do 2º grau, devemos resolver pela fórmula de Báskara.

Δ = b² - 4.a.c
Δ = (-20)² - 4 . 1 . 96

Δ = 400 - 384

Δ = 16

t = [-b +/- ⎷Δ] /2a

t =[ -(-20) +/- ⎷16]/2 . 1

t = [20 +/- 4]/2

t' = [20 + 4]/2     

t'= [24]/2

t’ = 12s

e 

t" = [20 - 4]/2

t" = 16/2

t’’ = 8s

O intervalo de tempo existente entre as passagens do projétil pela altura 480m equivale à 4s (12-8), pois na subida o tempo é de 8 s, e na descida é de 12s.

3) Lança-se um projétil com velocidade de 40 m/s, formando um ângulo 30º com a horizontal. Desprezando-se a resistência do ar, ele atingirá a altura máxima após quanto tempo?

Resolução:

Voy = Vo.sen30°

Voy = 40.1/2

Voy = 20 m/s

A velocidade no eixo y é igual a zero quando o projétil atingir a altura máxima:

t = Voy/g

0 = 20/10

t = 2 s

Resposta: A altura máxima será atingida após 2 s.

4) Um bloco de 250 g é arremessado com velocidade de 10 m/s, num ângulo de 30° com o solo. Determine as componentes vertical e horizontal da velocidade do bloco. Dado: sen 30° = 0,5 e cos 30° = 0,8

Resolução:

Na vertical, temos:

Voy = v . senθ

Voy = 10 . sen30°

Voy = 10 . 0,5

Voy = 5 m/s

Na horizontal, temos:

Vox = V . cosθ

Vox = 10 . cos 30°

Vox = 10 . 0,8

Vox = 8 m/s

Assista a vídeo aula pelo link: https://youtu.be/ryScqdbctFA

Agora faça os exercícios.

Exercícios.

1) Uma pedra de massa 200 g e uma folha de papel são abandonadas simultaneamente, do repouso, de uma altura de 2m. Desprezando a resistência do ar, podemos afirmar que:

a) A pedra chega no chão primeiro.

b) A folha de papel chega no chão primeiro.

c) A pedra e afolha de papel chegam juntas no chão.

d) A ação da gravidade sobre a pedra é maior do que na folha de papel.

e) A força gravitacional é maior na folha de papel.

2) Um jogador de futebol chuta uma bola de massa 250 g com uma velocidade de 40 m/s, num ângulo de 60° com o solo. Desprezando a resistência do ar, podemos afirmar que a velocidade horizontal da bola é de: 

Dado: sen 60° = 0,8 e cos 60° = 0,5.

a) 20 m/s

b) 25 m/s

c) 32 m/s

d) 38 m/s

e) 40 m/s

3) Com relação ao exercício anterior, qual é a altura máxima atingida pela bola?

a) 47,8 m

b) 51,2 m

c) 20 m

d) 55 m

e) 62,4 m

4) Ainda em relação ao exercício 3, qual é o alcance da bola? Dado sen 120° = 0,8.

a) 100 m

b) 110 m

c) 120 m 

d) 128 m

e) 130 m

5) Um atleta ao arremessar  um dardo, procura fazê-lo imprimindo a maior força possível. Porém o ângulo em que ocorre o arremesso interfere no alcance do dardo. O arremesso perfeito deve ocorrer em um ângulo de:

a) 40°

b) 35°

c) 60°

d) 75°

e) 45°