Física nuclear: radioisótopos e tempo de meia vida.

 Recomendações aos alunos:

* Leiam com atenção e observem os exemplos.

* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.

* Façam pesquisas em livros didáticos ou pela internet.

* Identifiquem as atividades com a data de postagem, nome, série, turma e nº de chamada (se possível).

* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br

* Data de entrega: até 29/09.

Olá pessoal! Que todos estejam bem.

Nessa semana vamos continuar o estudo de física nuclear estudando os radioisótopos e o tempo de meia vida de um núcleo radioativo.

Radioisótopos são isótopos radioativos de um elemento químico.

Isótopos são elementos químicos com mesmo número atômico e número de massa atômica diferentes.

Os Radioisótopos se referem a Isótopos que emitem radiação, ou seja, Isótopos radioativos.

Isótopos são átomos com o mesmo número atômico e diferente número de massa, mas como saber se são radioativos?

Conheça alguns:

Isótopos do Hidrogênio: 

 

Observe que os isótopos do elemento Hidrogênio possuem o mesmo número atômico (1), mas diferentes massas. O isótopo com massa 1 é o mais comum e não é radioativo. Já o isótopo com número de massa 2 é radioativo e dá origem às bombas de hidrogênio, e o isótopo com massa 3, ocorre em quantidades menores e é também radioativo.

Isótopos do Carbono:



O isótopo de Carbono 14 é um radioisótopo artificial, embora também exista na atmosfera, já o Carbono 12 é o mais comum na natureza, está presente no diamante, na grafite, etc.

O Carbono 14 é responsável por decifrar a idade de fósseis antigos, e por isso é elemento base na Arqueologia.

Isótopos do Urânio:



O isótopo de Urânio 238 não é radioativo, mas o 235 sim, e é usado para construir os reatores nucleares e as bombas atômicas.

Isótopos do Cobalto:



O Cobalto com número de massa 59 é o isótopo natural, já o Cobalto 60 é fabricado de modo artificial pelo bombardeamento do isótopo 59 com nêutrons. Este último é aplicado no tratamento de tumores. Veja a figura que ilustra o processo de bombardeamento do átomo de Cobalto:


Repare que um nêutron (indicado pela seta vermelha) colide com o núcleo de Cobalto modificando-o, neste instante ele adquire a propriedade radioativa e passa a emitir raios gama (indicado pela seta preta à direita).

O Cobalto 59 possui 27 prótons e 32 nêutrons (27+32 = 59), com o ganho de mais um nêutron passa a adquirir massa total = 60.

Os radioisótopos são muito úteis na agricultura, na engenharia, na medicina, etc., é importante lembrar que apresentam um alto grau de periculosidade e por isso são manipulados somente com o auxílio de robôs.

A radioatividade tem larga aplicação em nossa sociedade; portanto, na medicina não poderia ser diferente. A forma de radiação mais conhecida em diagnósticos médicos é a radiografia dos ossos através do uso de raios X. Além disso, usam-se isótopos para diagnósticos, tratamentos e detecção de drogas e hormônios no organismo.

Na medicina, é comum introduzir no organismo de alguns pacientes radioisótopos artificiais, denominados radiotraçadores. Eles recebem esse nome porque, ao serem transportados pelo corpo da pessoa, emitem radiações que permitem seu monitoramento, sabendo por onde passaram e onde se depositaram. Isso permite que o radiologista faça um mapeamento de órgãos.

Um exemplo de radioisótopo é o iodo-131 que é usado no tratamento de câncer de tireoide, pois, por se acumular nesse órgão, suas radiações gama destroem as células cancerígenas. Abaixo temos um quadro com exemplos de outros radioisótopos e sua utilização na medicina:

Além disso, é possível produzir imagens para os médicos analisarem, pois as radiações beta e gama incidem sobre filmes fotográficos. As imagens também são geradas por radioisótopos emissores de pósitrons e assim é possível detectar se a lesão em questão é benigna ou maligna.

Um tomógrafo usado para esse fim é o PET, sigla que vem do inglês, pósitron emission tomography, isto é, Tomografia por Emissão de Pósitron. O paciente submetido a esse exame recebe uma injeção com radioisótopo emissor de pósitron ligado a uma molécula que tem afinidade com o órgão do paciente que será estudado. Normalmente o radioisótopo utilizado é o flúor-18 com período de meia-vida de apenas 108 min. Ao redor do paciente estarão detectores de radiação que detectarão a emissão de ondas eletromagnéticas dos pósitrons que colidem com os elétrons. Dessa forma, o órgão é mapeado.

É claro que para cada caso deve haver uma avaliação médica criteriosa que decidirá se o benefício será maior que o risco, visto que a radiação também pode danificar células boas.

A radioatividade é aplamante utilizada na medicina

Publicado por: Jennifer Rocha Vargas Fogaça

A radioatividade vem sendo usada na agricultura de diversas formas, sendo que uma delas é na conservação de alimentos. A irradiação de frutas, legumes, cereais, frutos do mar, entre outros, diminui a quantidade de fungos e bactérias, aumentando, assim, seu tempo de conservação. Isso porque a multiplicação desses microrganismos é um dos principais causadores do apodrecimento dos alimentos.

Normalmente o alimento é irradiado por raios gama e beta de elementos radioativos, principalmente o cobalto 60; além também de sofrer radiação ionizante proveniente de raios X e elétrons acelerados. O alimento costuma ficar exposto a essa fonte de radiação, mas sem ter contato direto com tal elemento. Além disso, essa radiação é controlada, ou seja, acontece por um tempo prefixado e com objetivos bem determinados.

Por exemplo, se o alimento for submetido a uma radiação de 200 000 a 500 000 rad, ocorre a pasteurização do alimento, ou seja, ele vai ter mais tempo de conservação, mas desde que seja guardado em embalagens especiais ou em baixas temperaturas. No entanto, se essa radiação for maior, entre 2 e 4 milhões de rad, ocorre o que é chamado de esterilização, sendo que o alimento poderá ser conservado por mais tempo mesmo em temperatura ambiente.

Para citar apenas dois exemplos, uma batata irradiada pode durar até um ano sem apodrecer ou brotar e um peixe também pode ser conservado por mais de nove meses; tudo isso em temperatura ambiente!

Outro fator que aumenta o seu tempo de conservação é que a radiação pode alterar a estrutura molecular das frutas e legumes e inibir sua maturação por alterar processos fisiológicos das plantas.

Esse tratamento vem sendo eficaz e é adotado em inúmeros países, inclusive no Brasil, porque apesar de existirem outros meios de conservação, como a pasteurização térmica e a conservação refrigerada, alguns alimentos (tais como carnes, peixes, mariscos, aves, etc.) não podem ser submetidos a esses tratamentos. Desse modo, a irradiação desses alimentos se torna uma boa alternativa.

Outro benefício é o fato de esses alimentos permanecerem conservados mesmo em lugares agressivos em termos de temperatura, salinidade, umidade e outros fatores pelos quais passam principalmente os tripulantes de navios que ficam vários dias no mar, além do fato de que se eles vierem a naufragar esses alimentos terão mais tempo de vida, podendo alimentá-los e salvar suas vidas. O mesmo se aplica ao caso dos soldados do Exército, Marinha ou Aeronáutica.

Um ponto negativo visto até o momento é que o sabor e aroma do alimento sofrem algumas alterações.

O leite e seus derivados, além de alimentos muito gordurosos, não podem ser irradiados, pois sofrem reações de oxidação e ficam rançosos.

Outro uso da radiação na agricultura é na determinação da absorção de fertilizantes pelas plantas. Por exemplo, o P-32 é usado como radiotraçador, detectando quais partes da planta utilizou o nutriente. Há também o uso da radioatividade no controle de insetos e na verificação da autenticidade. Por exemplo, a determinação da razão isotópica estável do carbono 13 é usada para verificar se o mel é mesmo puro ou se foi adulterado com xarope de milho ou cana de açúcar.

A maioria das pessoas pensa que as aplicações pacíficas da radioatividade se restringem apenas ao campo médico. Porém, além dos tratamentos médicos, as indústrias também vêm utilizando bastante a radioatividade. Conheça alguns desses usos:

• Radiografia de peças metálicas ou gamagrafia industrial: esse processo se dá pela impressão de radiações gama em filme fotográfico. Essa aplicação de radioisótopos é importante até mesmo para salvar vidas, pois as empresas aéreas realizam a gamagrafia das partes metálicas e das soldas essenciais dos aviões, que são sujeitas a mais esforços, como asas e turbinas. Com isso, é possível inspecionar os aviões e verificar se há fadiga em alguma de suas partes.

Outro exemplo importante do uso da gamagrafia se dá na construção de gasodutos, em que é possível detectar se há defeitos como bolhas e rachaduras na tubulação ou nas soldas.

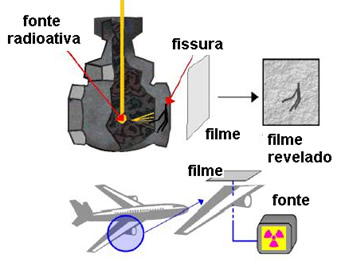
• Detecção de vazamentos: para detectar pequenos vazamentos em tubulações de água, costumava-se usar escavadeiras para retirar a terra. No entanto, hoje há um processo muito menos trabalhoso, em que se usam os radioisótopos 24Na ou o 131I. O sódio radioativo pode ser introduzido na tubulação na forma de carbonato, que é solúvel em água. O contador Geiger é então usado para rastrear as emissões desse isótopo que, no local do vazamento, registra emissões muito superiores às regulares dos lugares onde não há vazamento.
• Falhas de lâminas: os radioisótopos também são usados para medir a espessura e indicar falhas em lâminas metálicas. Isso é feito através da instalação de uma fonte de radiações gama, como o cobalto 60, em um lado da lâmina; e um contador Geiger, do outro lado. A radiação atravessa a lâmina, chegando ao contador; assim, a leitura de variações revelará irregularidades na espessura.
• Em pneus: o 32P é um radioisótopo usado para medir o desgaste de frisos de pneus.
• Em linhas de produção: um exemplo é a forma como é feita a indicação do nível de um líquido em uma garrafa. De um lado da garrafa fica uma fonte radioativa e do outro lado coloca-se um detector ligado a um aparelho de medição. Quando o líquido alcança a altura da fonte, a maior parte da radiação emitida pela fonte é absorvida por ele e deixa de chegar ao detector, o que significa que o líquido atingiu o nível correto e a esteira pode andar.

• Para evitar derramamento: para diminuir o risco de derramamento, são utilizadas fontes seladas, acondicionadas em caixas de aço inoxidável hermeticamente fechadas.

• Esterilização: como as radiações gama ultrapassam os materiais menos densos, estes podem ser utilizados para esterilizar materiais cirúrgicos e alimentos. Esse processo é utilizado principalmente pela indústria farmacêutica, pois alguns materiais descartáveis (como seringas, gazes e luvas cirúrgicas) não suportam altas temperaturas. Assim, esses produtos são esterilizados com fontes radioativas.

A radioatividade possui larga aplicação na indústria

Por: Jennifer Rocha Vargas Fogaça

Tempo de meia vida (T1/2): é o tempo necessário para que a radiação de um núcleo radioativo caia pela metade.

Meia-vida, também conhecida como período de semidesintegração, é o tempo necessário para que metade do número de átomos do isótopo radioativo presente em uma amostra desintegre-se.

→ Desintegrações

A desintegração não está relacionada com a extinção do átomo, ou seja, o átomo não deixa de existir. Na verdade, o que ocorre é o decaimento natural que o átomo sofre. No decaimento, o átomo (X), ao emitir radiação alfa e beta, transforma-se automaticamente em um novo elemento químico (Y), o que ocorre incessantemente até que o átomo deixe de ser radioativo (átomo estável).

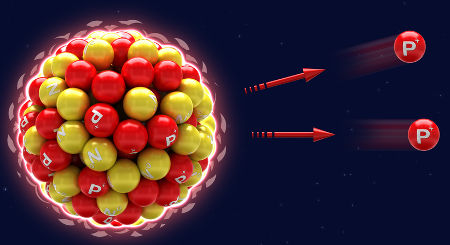
Representação do decaimento natural a partir de emissões alfa (prótons)

X → α + Y

Ou

X → β + Y

Se o átomo Y formado no decaimento for radioativo, novas radiações alfa e beta serão emitidas do núcleo desse átomo. Quando se chega à meia-vida de um material, sabemos que metade dos átomos que existiam na amostra tornou-se estável.

→ Meia-vida dos isótopos

Cada isótopo radioativo apresenta uma meia-vida diferente. Essa meia-vida pode ser expressa em segundos, minutos, horas, dias e anos. A tabela abaixo traz a meia-vida de alguns isótopos radioativos:

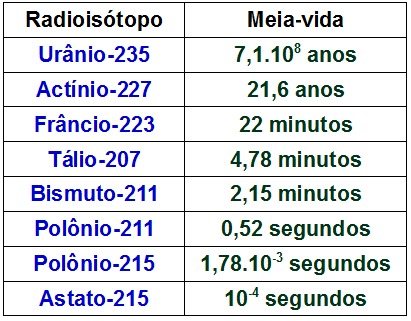
Valores da meia-vida de alguns radioisótopos

→ Fórmulas utilizadas no estudo de meia-vida

O período de meia-vida é representado pela sigla P. Já o tempo que um material sofreu desintegração é representado por t. Assim, se conhecemos a meia-vida e o tempo de desintegração (representado por x), podemos afirmar por quantas meias-vidas um material passou até certo momento. Isso é feito por intermédio da relação abaixo:

t = x . P

Onde:

t = tempo decorrido de desintegração

x = Nº de meias vidas

P = tempo de meia vida

Com esse conhecimento, podemos ainda determinar o número de átomos que resta após o período de meia-vida a partir da expressão:

n = n_o
     2^x

• n = número de átomos radioativos que resta na amostra;

• n_o = número de átomos radioativos que havia na amostra;

• x = número de meias-vidas que se passaram.

Além do cálculo do número de átomos propriamente dito, a desintegração ou a diminuição da quantidade do material radioativo após um período de meia-vida pode ser expressa das seguintes formas:

→ Em forma de porcentagem:

P_r = P_o
      2^x

• P_r = porcentagem de material radioativo que resta na amostra;

• P_o = porcentagem inicial de material radioativo que havia na amostra (sempre será 100%);

• x = número de meias-vidas que se passaram.

→ Em forma de massa:

m = m_o
     2^x

• m = massa do material radioativo que resta na amostra;

• m^o = massa do material radioativo que havia na amostra;

• x = número de meias-vidas que se passaram.

→ Em forma de números fracionários (fração):

F = N_o
      2^x

• F = fração referente ao material radioativo que resta na amostra;

• N_o = quantidade referente ao material radioativo que havia na amostra, que, na realidade, é sempre o número 1 no caso de exercícios que envolvem fração;

• x = número de meias-vidas que se passaram.

→ Exemplos de cálculos envolvendo meia-vida

Acompanhe agora alguns exemplos de cálculos que envolvem meia-vida:

Exemplo 1: Após 12 dias, uma substância radioativa tem sua atividade reduzida para 1/8 da inicial. Qual é a meia-vida dessa substância?

Dados do Exercício:

• Meia-vida (P) = ?

• Tempo total (t) = 12 dias

• Fração restante (F) = 1/8

• Quantidade inicial (N_o) = 1

Temos que determinar o número de meias-vidas (x) sofridas pelo material na seguinte expressão:

F = N_o
      2^x

1 = 1
8   2^x

2^x.1 = 8.1

2^x = 8

2^x = 2³

x = 3

Em seguida, determinamos o valor da meia-vida utilizando o valor de x encontrado e o tempo fornecido pelo enunciado:

t = x.P

12 = 3.P

12 = P
3     

P = 4 dias

Exemplo 2: Um elemento radioativo tem meia-vida igual a 5 minutos. Dispondo-se de 6 g desse elemento, qual será a sua massa após 20 minutos?

Dados do Exercício:

• Meia-vida (P) = 5 minutos

• Massa inicial (m_o) = 6 g

• Tempo total = 20 minutos

• Massa restante (m) = ?

Inicialmente determinamos o valor da quantidade de meias-vidas (x) que o material sofreu por meio do tempo e da meia-vida fornecidos:

t = x.P

20 = x.5

20 = x
5      

x = 4

Por fim, calculamos a massa restante por meio do valor de x e da massa inicial na seguinte expressão:

m = m_o
       2^x

m = 6
       2⁴

m = 6
      16

m = 0,375 g

Exemplo 3: Um elemento radioativo tem uma meia-vida de 20 minutos. Após quanto tempo a sua massa se reduzirá para 25% da massa inicial?

Dados do Exercício:

• Meia-vida (P) = 20 minutos

• Tempo total (t) = ?

• Porcentagem restante (P_r) = 25%

• Porcentagem inicial (P_o) = 100%

Temos que determinar o número de meias-vidas (x) sofridas pelo material na seguinte expressão:

P_r = P_o
       2^x

25 = 100
       2^x

2^x.25 = 100

2^x = 100
       25

2^x = 4

2^x = 2²

x = 2

Em seguida, determinamos o valor do tempo utilizando o valor de x encontrado e a meia-vida fornecida pelo enunciado:

t = x.P

t = 2.20

t = 40 minutos

O gráfico da meia-vida do radioisótopo é sempre uma curva descendente em virtude do decaimento

A descoberta de um fóssil é um momento de realização para os arqueólogos, daí se começa o processo de datação do achado e quanto mais antiga for a relíquia maior será seu valor para a paleontologia. Mas, como é possível descobrir a idade de um fóssil?

A química está presente nesse processo, mais precisamente o elemento Carbono. A datação de um fóssil pode ser feita com base no percentual já conhecido do Carbono-14 (C14) em relação ao Carbono-12 (C12) da matéria viva (sem decomposição).

O carbono 14 é um isótopo radioativo natural do elemento carbono, recebendo esta numeração porque apresenta massa atômica 14. Esse isótopo apresenta dois nêutrons a mais no seu núcleo que o isótopo estável carbono 12.

O C14 é formado continuamente na atmosfera e é resultante do processo de bombardeio de raios cósmicos. Forma-se nas camadas superiores da atmosfera onde os átomos de nitrogênio-14 são bombardeados por neutrons contidos nos raios cósmicos e por isso é denominado de carbono radioativo ou radioisótopo. Ele entra no processo de fotossíntese e em conseqüência disso todos os seres vivos possuem em sua composição geral certa porcentagem de C14, ainda que em pequena quantidade. O C12 é o carbono comum (não-radioativo).

Quando o ser vivo morre inicia-se uma diminuição da quantidade de carbono-14 devido a sua desintegração radiativa. A meia-vida do C14 é de 5.740 anos, este é o tempo que o C14 leva para transmutar metade dos seus átomos em C12, os cientistas então se baseiam no cálculo comparativo entre a quantidade habitual encontrada na matéria viva, e aquela que foi descoberta no fóssil, determinando assim a idade do mesmo.

Exemplo: Em um fóssil de 11.480 anos, é encontrado somente ¼ da quantidade habitual de C14. Já em um fóssil de 22.960 anos deve-se encontrar 1/8 da quantidade normal do radioisótopo.

Fóssil de um Dinossauro Rex.

Exemplos.

1) O criptônio-89 possui o tempo de meia-vida igual a 3,16 minutos. Dispondo-se de uma amostra contendo 4,0 . 10²³ átomos desse isótopo, ao fim de quanto tempo restarão 1,0 . 10²³ átomos?

Resolução:

T1/2 = 3,16 min.

No = 4 . 10²³

N = 1 . 10²³

x =?

n = n_o
     2^x

^{1 . 10²³ = 4 . 10²³/}2^x

2^{x = 4.10²³/1.10²³}

^{2x = 4}

^{2x = 2²}

^{x = 2}

^{Como se passaram 2 meias vidas, e cada meia vida é de 3,16 min, temos:}

^{3,16 . 2 = 6,32 min.}

^{Resposta: Ao final de 6,32 min.}

²⁾ O césio-137 possui meia-vida de 30 anos. Se tivermos 12 g desse elemento, após quanto tempo essa massa será reduzida para 0,75 g?

Resolução:

T1/2 = 30 anos

Mo = 12 g

M = 0,75 g

x = ?

M = Mo/2^x

^{0,75 = 12/}2^x

^{2x = 12/0,75}

^{2x = 16}

^{2x = 2⁴}

^{x = 4 meias vidas.}

^{Como cada meia vida é de 30 anos, temos:}

^{30 . 4 = 120anos.}

^{Resposta: Serão necessários 120 anos.}

^{3) Um determinado radioisótopo emite radiação beta(e-) e reduz sua radioatividade a 1/4 da inicial. O tempo decorrido nessa redução foi de 16 dias. Determine a meia vida desse radioisótopo.}

^Resolução:

^{Para que a radiação chegue e 1/4 da radiação inicial passaram-se duas meias-vidas:}

^{1→1/2(1ª meia-vida)→ 1/4 (2ª meia-vida)}

^{Se duas meias-vidas são 16 dias, temos que uma meia vida equivale a 8 dias.}

^{F = No/2˟}

^{1/4 = 1/2˟}

^{2˟ = 4}

^{2˟ = 2²}

^{x = 2 meias vidas}

^{Como, t = x.T1/2}

^{16 = 2. T1/2}

^{16/2 = T1/2}

^{T1/2 = 8 dias}

^{Pode-se fazer das duas maneiras.}

^{Resposta: O tempo de meia-vida (T1/2) é de 8 dias.}

^{Agora façam os exercícios.}

^Exercícios.

¹⁾ Pesquisadores recuperaram DNA de ossos de mamute (Mammuthus primigenius) encontrados na Sibéria, que tiveram sua idade de cerca de 28 mil anos confirmada pela técnica do CARBONO-14.

FAPESP. DNA do mamute é revelado. Disponível em: http://agencia.fapesp.br. Acesso em: 13 ago. 2012(adaptado).

A técnica de datação apresentada no texto só é possível devido à

a) transformação de carbono-12 em carbono-14 ao longo dos anos.
b) decomposição de todo o carbono-12 presente no organismo após a morte.
c) fixação maior do carbono-14 nos tecidos de organismos após a morte.
d) emissão de carbono-12 pelos tecidos de organismos após a morte.
e) proporção conhecida entre carbono-14 e carbono-12 na atmosfera ao longo dos anos.

2) O isótopo radioativo do iodo  produzido artificialmente é usado no diagnóstico do câncer na tireóide. Quando se ingere iodo, ele fica acumulado na tireóide. Em estado normal, a glândula absorve pouco o iodo radioativo, mas, afetada pelo câncer, absorve-o em maior quantidade, podendo ser detectado por meio de detectores de radioatividade. Sabendo-se que o tempo de meia-vida do isótopo  é de 8 dias, e que, após 40 dias, encontra-se uma massa de 0,5 g, qual a massa inicial do isótopo, em gramas?

a) 16 g

b) 14 g

c) 12 g

d) 10 g

e) 8 g

3) Vinte gramas de um isótopo radioativo decrescem para cinco gramas em dezesseis anos. A meia-vida desse isótopo é:

a) 4 anos.
b) 16 anos.
c) 8 anos.
d) 10 anos.
e) 32 anos.

4) O Iodo-125, variedade radioativa do Iodo com aplicações medicinais, tem meia-vida de 60 dias. Quantos gramas de Iodo-125 restarão após seis meses, com base em uma amostra contendo 2 g do radioisótopo?

a) 1,50 g

b) 0,25 g

c) 0,66 g

d) 0,75 g

e) 0,10 g

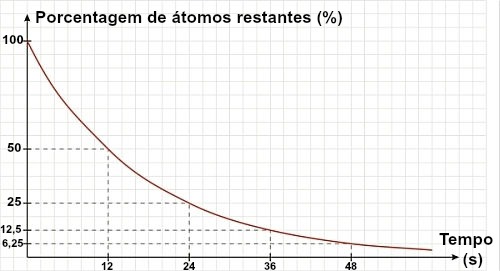
5) Um osso encontrado em uma caverna apresenta uma taxa de carbono 14 igual a 6,25 % da taxa existente em um animal vivo e na atmosfera. Sabendo que o tempo de meia-vida do carbono 14 é de 5730 anos, assinale a alternativa que corresponde aos anos que se decorreram após a morte do indivíduo.

a) 5 730 anos.

b) 11 460 anos.

c) 17 190 anos.

d) 22 920 anos.

e) 28 650 anos.