Olá turma! 

Espero que todos estejam bem! 

Prof.ª: Monica   

Disciplina :Matemática   

Período: 19/08/20 á 26/08/2020 

Recurso :Assistir as aulas no Centro de Mídias São Paulo realizadas em 07 e 08/07/2020  

Dúvidas segue meu e –mail: monicax@prof.educacao.sp.gov.br e whatsapp (11) 99870 - 3595  

Habilidade:( EF09MA19) Resolver e elaborar situações problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos) em situações como determinar medida de terreno.  

Atenção:  

*As atividades que forem entregue na escola, faça em folha separada e assim receberam nota e presença. 

*se for entrega pelo e-mail ou whatsapp que está logo acima, tire foto e envie e não esquecer do nome e série.  

*acompanhe as aulas do Centro de Mídias ajudará nas atividades propostas. 

* Copiar e resolver as questões propostas abaixo. 

*O envio dessa atividade contará como sua presença dessa semana  

* Entrega da atividade :26/08/2020

     Área de Figuras Planas 

     As áreas das figuras planas medem o tamanho da superfície da figura. Desse modo, podemos pensar que quanto maior a superfície da figura, maior será sua área. 

    A geometria plana é a área da matemática que estuda asa figuras planas. Ou seja, aquelas que possuem comprimento e largura, sendo figuras bidimensionais (duas dimensões). 

   Principais Figuras Planas  

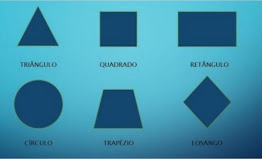
 Antes de apresentar as fórmulas das áreas das figuras planas, devemos atentar para cada uma delas: 

Triângulo = polígono formado por três lados. Quadrado = quadrilátero regular formado por quatro lados congruentes (mesma medida). 

Retângulo=quadrilátero formado por quatro lados, dois deles na vertical e dois na horizontal. 

Círculo= figuras plana também chamada de disco, que apresenta uma forma circular. O raio do círculo representa a medida entre o ponto central da figura e uma das extremidades. O diâmetro equivale duas vezes o raio. 

Trapézio=quadrilátero notável com dois lados e base paralelas, donde uma é maior e outra menor. 

Losango=quadrilátero equilátero formado por quatro lados iguais. 

Fórmula das Áreas das figuras Planas 

      Confira abaixo ás fórmulas para os cálculos de área: 

                    

   Atenção! 

  Vale relembrar que a área e o perímetro são dois conceitos utilizados na geometria plana, no entanto, apresentam diferenças. 

   Área: tamanho da superfície da figura. O valor da área será, dado sempre em ,𝑐𝑚2   ,      𝑚2 ou k𝑚2. 

   Perímetro: soma de todos os lados da figura. O valor do perímetro será dado sempre em cm, m ou km.  

Exercícios resolvidos 

1) Determine a área de um triângulo cuja base mede 10cm e a altura também medem 10cm. 

Solução: 𝐴 = 𝑏.ℎ 2                A = 10.10 2               𝐴 = 100 2 

             𝐴 = 50𝑐𝑚2  

2) O lado de um quadrado mede 8cm. Agora Calcule sua área. 

Solução:  𝐴 = 𝐿2 

                 𝐴 = 82                   

                 A = 64 𝑐𝑚2 

3) Qual é área de um losango que possui diagonal maior medindo 10cm e diagonal menor medindo 7cm? 

Solução: 𝐴 = 𝐷.𝑑 2                  A = 10.7 2                 𝐴 = 70 2   

                 𝐴 = 35𝑐𝑚2 

4)Uma quadra oficial de vôlei tem dimensões de 9m por 18m. Determine a área desta quadra. 

Solução: A = b. h 

         A = 18.9         𝐴 = 162𝑚2  

Então, essa quadra têm o formato de um retângulo.  

5) Calcule a área de um trapézio de altura 5cm e bases de 8cm e 3cm.     

  Solução: A = (B + b) / 2.h                A = (8 + 3) / 2.5                A = 11/ 2. 5                A = 5,5 .5                A = 27,5 𝑐𝑚2  

Área do Círculo 

    Para calcular a área do círculo devemos utilizar a seguinte fórmula:                               

    A = π. 𝑟2  Onde π: constante pi (3,14)                                     r : raio   

   Fique atento?  

          Lembre-se –se que o raio ( r ) corresponde a distância entre o centro e a extremidade do círculo.  

       

        Já o diâmetro é um segmento de reta que passa pelo centro do círculo, dividindo –o em duas metades iguais. Dito isso, o diâmetro equivale duas vezes o raio (2r).  

Perímetro do Círculo   

       O perímetro é um conceito da matemática que mede o comprimento (contorno) de determinada figura. Em outras palavras, o perímetro é a soma de todos os lados de uma figura geométrica.        No caso do círculo, o perímetro é chamado de circunferência e é calculado pelo dobro da medida do raio (2r). Assim, o perímetro da circunferência é medida pela fórmula: 

 

Diferença entre Círculo e Circunferência 

            Embora a maioria das pessoas acreditam que o círculo e a circunferência são as mesmas figuras, elas possuem diferenças. Enquanto a circunferência é a linha da curva que limita o círculo e uma figura plana limitada pela circunferência. 

Exemplo :Calcule a área do círculo que apresenta 3cm de raio. Para calcular a área basta colocar o valor na fórmula:  

                𝐴 = 𝜋.𝑟2                 𝐴 = 𝜋.32                   A = π. 9 𝑐𝑚2                 A= 3,14. 9                   𝐴 = 28,3𝑐𝑚2  Aproximadamente    

Exemplo: Qual é a área de um círculo cujo diâmetro mede 10cm? Primeiramente devemos lembrar que o diâmetro é duas vezes o valor do raio. Logo, o raio desse círculo mede 5cm.                 𝐴 = 𝜋.𝑟2                𝐴 = 𝜋.52              A = 25.π              A = 25. (3,14)              𝐴 = 78,5 𝑐𝑚2 Aproximadamente    

          Assista os Vídeos  abaixo:  

          

                   

Questões  

1) Calcule a área de cada figura: 

a)                                          

                                                         

b)

c)

d)

2) Pedro confecciona papagaios usando papel de seda e pedaços finos de madeira. Depois de pronto, um de seus papagaio ficou conforme mostra a figura abaixo. Quantos centímetros quadrados de papel de seda Pedro gastou para confeccionar esse papagaio? 

                                                                           

3) Para obter uma peça com forma de trapézio, um marceneiro cortou uma chapa de madeira retangular conforme indicado. Quantos metros quadrados foram retirados dessa chapa de madeira?  

 4)  Seja um quadrado medindo 10cm cada um de seus lados. Calcule a área desse quadrado.  

5) A escola “Aprender Feliz “vai pintar um triângulo na parede do pátio, para que os alunos o decorem como uma árvore de natal. No desenho abaixo, podemos ver como ficará a parede, depois de pintada.Com base nas dimensões da parede registrada no desenho podemos afirmar que a área a ser pintada será de: 

                               

                                             

6) Para fazer uma pequena horta, Pedro dividiu uma área retangular de 3,0m de comprimento por 3,6m de largura em seis partes iguais, como mostra a figura abaixo: Qual é a área de cada parte? 

              

                                                                     

7) Qual é a medida do raio de um terreno circular, cuja sua área mede 1017,36 metros quadrados?  

8) Quantos metros quadrados de pisos serão gastos para revestir uma área circular cujo raio mede 6 metros?

                                                     Bons estudos !