* Leia com atenção e observe os exemplos.
* Assistam às vídeo aulas pelo CMSP, TV, plataforma Stoodi.
* Faça pesquisas em livros didáticos ou pela internet.
* Identifique as atividades com nome, série, turma, n° de chamada (se possível).
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 18/08.
Momento de uma força
Imagine uma pessoa tentando abrir uma porta, ela precisará fazer mais força se for empurrada na extremidade contrária à dobradiça, onde a maçaneta se encontra, ou no meio da porta?
Claramente percebemos que é mais fácil abrir ou fechar a porta se aplicarmos força em sua extremidade, onde está a maçaneta. Isso acontece, pois existe uma grandeza chamada Momento de Força 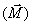 , que também pode ser chamado Torque.
, que também pode ser chamado Torque.
Esta grandeza é proporcional a Força e a distância da aplicação em relação ao ponto de giro, ou seja:
A unidade do Momento da Força no sistema internacional é o Newton-metro (N.m)
Como este é um produto vetorial, podemos dizer que o módulo do Momento da Força é:
Sendo:
M= Módulo do Momento da Força.
F= Módulo da Força.
d=distância entre a aplicação da força ao ponto de giro; braço de alavanca.
sen θ=menor ângulo formado entre os dois vetores.
Como 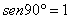 , se a aplicação da força for perpendicular à d o momento será máximo;
, se a aplicação da força for perpendicular à d o momento será máximo;
Como 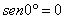 , quando a aplicação da força é paralela à d, o momento é nulo.
, quando a aplicação da força é paralela à d, o momento é nulo.
E a direção e o sentido deste vetor são dados pela Regra da Mão Direita.
O Momento da Força de um corpo é:
- Positivo quando girar no sentido anti-horário;
- Negativo quando girar no sentido horário;
Exemplo:
1) Qual o momento de força para uma força de 10N aplicada perpendicularmente a uma porta 1,2m das dobradiças?
2) Vejamos a figura abaixo. Na figura temos dois blocos cujas massas são, respectivamente, 4 kg e 6 kg. A fim de manter a barra em equilíbrio, determine a que distância x o ponto de apoio deve ser colocado. Suponha que inicialmente o ponto de apoio esteja a 40 cm da extremidade direita da barra.
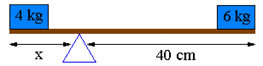
Resolução:
Para que a barra se mantenha em equilíbrio o momento do conjunto tem que ser igual a zero.
M1=M2
F1.d1=F2.d2
4 . x = 6 .40
F1.d1=F2.d2
4 . x = 6 .40
3) Um rapaz de 900 N e uma garota de 450 N estão em uma gangorra. Das ilustrações abaixo, a que representa uma situação de equilíbrio é:
a)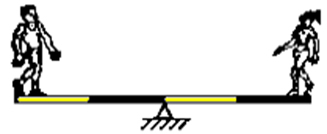

b)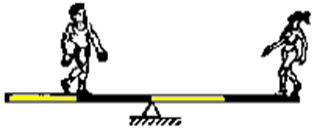

c)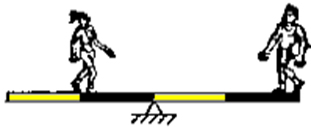

d)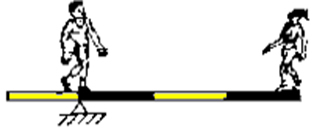

e)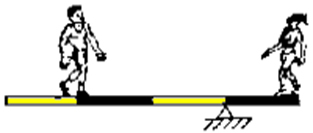

Resolução:
Para resolver essa situação basta igualar os momentos, isto é, o momento de força do rapaz é igual ao momento de força da moça, ambos sobre a barra, portanto, temos:
Mrapaz=Mmoça
Fr.d1=Fm.d2
Fr.d1=Fm.d2
Como o peso do homem é o dobro do peso da moça, ele deve estar na metade da distância do apoio.
900 . 1 = 450 .2
Alternativa B
4) A figura representa a força aplicada na vertical, sobre uma chave de boca, por um motorista de caminhão tentando desatarraxar uma das porcas que fixa uma roda.

O ponto de aplicação da força dista 15 cm do centro da porca e o módulo da força máxima aplicada é F = 400 N. Nesta situação, suponha que o motorista está próximo de conseguir desatarraxar a porca. Em seguida, o motorista acopla uma extensão à chave de boca, de forma que o novo ponto de aplicação da força dista 75 cm do centro da porca. Calcule o novo valor do módulo da força, F’, em newtons, necessário para que o motorista novamente esteja próximo de desatarraxar a porca.
Resposta:
M = F×d
Na primeira situação: M = 400 N × 15 cm = 6.000 N.cm
Na segunda situação: 6.000 = F × 75 cm
F = 80 N
5)
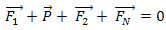
Na primeira situação: M = 400 N × 15 cm = 6.000 N.cm
Na segunda situação: 6.000 = F × 75 cm
F = 80 N
5)

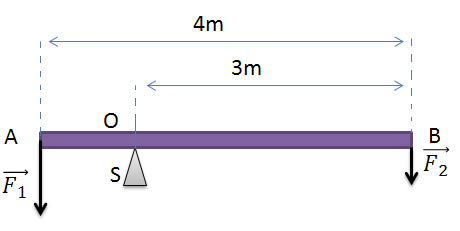
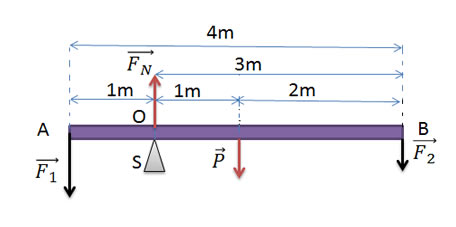
Na figura temos uma barra homogênea AB de peso 80 N, que está em equilíbrio sob ação das forças e , apoiadas no suporte S, no ponto O. Sendo = 200 N, qual será a intensidade de e da força normal exercida pelo suporte S sobre a barra?
(a) 40 N e 320 N
(b) 60 N e 320 N
(c) 40 N e 200 N
(d) 50 N e 200 N
(e) 200 N e 40 N
Resolução:
Letra A

Todas as forças que atuam na barra foram colocadas na figura. Como a barra é homogênea, todo o seu peso está em seu centro (centro de gravidade). Agora vamos aplicar as duas condições de equilíbrio.
1º: A soma de todos os momentos deve ser nula.
Como não sabemos o valor da força 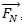 , vamos escolher a origem O como nosso centro de rotação, assim o momento de uma força da força
, vamos escolher a origem O como nosso centro de rotação, assim o momento de uma força da força 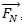 se torna nulo.
se torna nulo.
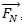 , vamos escolher a origem O como nosso centro de rotação, assim o momento de uma força da força
, vamos escolher a origem O como nosso centro de rotação, assim o momento de uma força da força 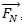 se torna nulo.
se torna nulo.
Como M = +F.d (se o momento de uma força tende a produzir rotação no sentido anti-horário em volta do polo de origem da rotação) e M = -F.d (se o momento de uma força tende a produzir rotação no sentido horário em volta do polo de origem da rotação), temos:
MF1 = + F1 .(1)
MP = - P . (1)
MF2 = - F2 . (3)
Para uma situação de equilíbrio, a soma do momento de todas as forças deve ser igual a zero, lembrando que MFN = 0, pois está no polo de rotação:
MF1 + MP + MF2 + MFN = 0
F1 .(1) - P . (1) - F2 . (3) + 0 = 0
200 . (1) – 80 . (1) - F2 . (3) = 0
200 – 80 – 3F2 = 0
3F2 = 120
F2 = 120/3
F2 = 40 N
Para que a barra esteja em equilíbrio, é necessária outra condição, a resultante das forças também tem que ser nula. Logo:
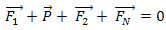
- F1 - P - F2 + FN = 0
FN = F1 + P + F2
FN = 200 + 80 + 40
FN = 320 N
Assista a vídeo aula sobre estática na plataforma Stoodi.
Agora faça os exercícios.
Exercícios.
1) Uma força de 200 N é aplicada perpendicularmente ao plano de uma porta, em uma distância de 50 cm do eixo de rotação dessa porta, que passa a girar no sentido anti-horário. O torque produzido por essa força é igual a:
a) + 100 N.m
b) - 100 N.m
c) + 10.000 N.m
d) + 0,50 N.m
e) - 2 N.m
2) Dois garotos brincam em uma gangorra de 10 m de comprimento que possui seu eixo de rotação exatamente em seu centro. Adotando a barra que compõe a gangorra como homogênea e sabendo que um garoto de 30 kg sentou-se na extremidade da direita, qual deverá ser a distância entre o segundo garoto e o eixo de rotação para que a gangorra mantenha-se em equilíbrio.
Dados: Massa do segundo garoto = 40 kg; Aceleração da gravidade = 10 m/s2.
a) 3,75 m
b) 4 m
c) 4,75 m
d) 4,5 m
e) 3,5 m
3) Analise as afirmações a respeito do momento de uma força.
I) O torque é uma grandeza escalar relacionada com a rotação de um sistema.
II) A força necessária para girar uma porta seria maior se a maçaneta fosse instalada próximo das dobradiças.
III) A única condição de equilíbrio existente está relacionada com a rotação de um sistema. Sendo assim, se a soma de todos os torques que atuam em um sistema for nula, haverá equilíbrio.
Está correto o que se afirma em:
a) I e II
b) II e III
c) II
d) III
e) I
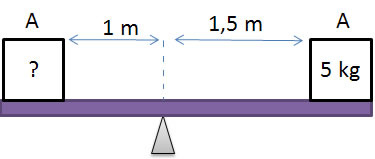
4)

Na figura acima, os dois blocos, A e B, estão em equilíbrio. Calcule a massa do bloco A, sabendo que a massa do bloco B é 5 kg. Considere 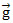 =10m/s².
=10m/s².
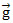 =10m/s².
=10m/s².
a) 6 Kg
b) 6,5 Kg
c) 7 Kg
d) 7,5 Kg
e) 8 Kg
5) Uma chave de boca tem 30 cm de comprimento. Ao aplicar uma força na extremidade dessa chave, o momento da força aplicada para girar um parafuso é de 6 N.m. Podemos afirmar que a força aplicada foi de:
a) 0,2 N
b) 2 N
c) 5 N
d) 10 N
e ) 20 N
Nenhum comentário:
Postar um comentário
Não esqueça de colocar seu nome completo e série/ano turma