Recuperação: formas de energia, suas transformações, potencia e trabalho.

Recomendações aos alunos:
* Leiam com atenção e observemos exemplos.
* Assistam às aulas pelo CMSP, TV, plataforma de estudos Stoodi e façam pesquisas em livros didáticos ou pela internet.
* Não esqueçam de identificar as atividades com nome, ano, turma e n° de chamada ( se possível ).
* Enviem as atividades para o E-mail: josecorreia@prof.educacao.sp.gov.br
* Data de entrega: até 28/07.

Recuperação.

Ola pessoal! Vamos revisar os conteúdos estudados nesse bimestre.

- Energia mecânica: é a energia associada ao movimento. É constituída por três diferentes formas de energia, energia cinética, energia potencial gravitacional e energia potencial elástica.

Fórmulas:

Em = Ec + Epg

Ec = m . v²

            2

Epg = m . g . h

Epe = K . x² 

              2

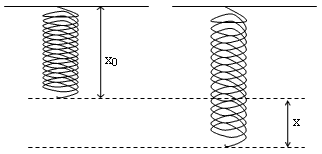
No S.I. a unidade de medida de energia é o joule (J). Em homenagem ao físico James Prescott Joule.

Onde:

Em = energia mecânica ( joule(J))

Ec = energia cinética (joule(J))

Epg = energia potencial gravitacional (joule(J))

Epe = energia potencial elástica (joule (J))

m = massa (quilograma (Kg))

v = velocidade (metros por segundo (m/s))

g = aceleração da gravidade metros por segundo ao quadrado (m/s²))

h = altura em relação ao solo (metros (m))

K = constante elástica (newton por metro (N/m))

x = deformação sofrida pela mola ou elástico (metros (m))

- Potencia: é a grandeza física que mede a rapidez com que um trabalho é realizado. 

No S.I. a unidade de medida de potencia é o watts (W). Em homenagem ao físico inglês James Watts.

Fórmula:

P = E 

      Δt

Onde:

P = potencia ( watts(W) )

E = energia ( joule (J))

Δt = tempo ( segundos (s))

Assim, temos que: 1W = 1J 

                                         1s

- Trabalho: ocorre quando ao se aplicar uma força em um objeto, este sofre um deslocamento.

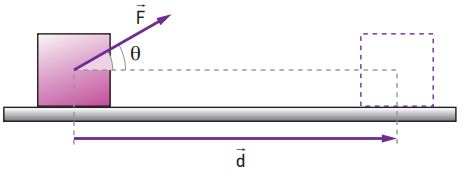
Fórmula:

T = F . d . cos Θ

Onde: 

T = trabalho da força ( joule (J))

F = força aplicada (newton (N))

d = distância percorrida pelo objeto (metros (m))

cos Θ = cosseno do ângulo formado entre a força e o deslocamento do objeto.

Exemplos.

1) Uma boneca de massa igual a 0,5 kg foi derrubada de uma janela do 3º andar, numa altura de 10 m do chão. Qual a energia cinética da boneca ao atingir o solo e qual a velocidade com que ela caiu? Considere a aceleração da gravidade como sendo 10 m/s2.

Resolução:

m = 0,5kg

h = 10m

g = 10m/s²

A energia potencial se transforma em energia cinética durante a queda, e no solo a energia cin ética é igual a energia potencial.

Ec = Epg

Epg = m . g . h

Epg =  0,5 . 10 . 10

Epg = 50J

Assim, temos: Ec = Epg = 50J

A velocidade com que a boneca chega ao solo é:

Ec =m . v² 

           2

50 = 0,5 . v² 

              2

50 . 2 = 0,5 . v²

100 = v²

 0,5

v² = 200

v = ⎷200

v ≅ 14,14 m/s

2) Numa montanha-russa, um carrinho com 300 kg de massa é abandonado do repouso de um ponto A, que está a 5,0 m de altura. Supondo que os atritos sejam desprezíveis e que g = 10 m/s², calcule:

a) o valor da velocidade do carrinho no ponto B;

b) a energia cinética do carrinho no ponto C, que está a 4,0 m de altura.

Resolução:

a) Aplicando o princípio da conservação da energia mecânica, temos:

Ema = Emb

Eca + Epga = Ecb + Epb

0 + m . g .h = m . v² + 0

300 . 10 . 5 = 300 . v²

                           2

50 = v²

        2

50 . 2 = v²

100 = v²

v = ⎷ 100

v = 10m/s.

b) Emb = Emc

Ecb + Epgb = ECc + Epc

m . v² + 0 = ECc + m. g . h

    2                 

300 . 10² = ECc + 300 . 10 . 4

       2

300 . 100 = ECc + 12000

       2

30000 = ECc + 12000

    2

15000 - 12000 = ECc

ECc = 3000J

                          

3) Imagine a seguinte situação: um operário da construção civil precisa carregar um saco de cimento de 50 kg. Ele levanta esse saco de cimento e se desloca por 20 metros na horizontal. Adote g = 10 m/s². Calcule o trabalho realizado pela força do operário sobre o cimento.

A resposta é zero. Embora o operário exerça uma força em módulo igual ao peso do saco de cimento, que é de 500 N, essa força é na vertical, enquanto seu deslocamento é na horizontal, ou seja, o ângulo entre a força e o deslocamento é 90°. Quando a força e o deslocamento formam um ângulo igual a 90°, o trabalho realizado por essa força é nulo. Veja: 

T = F . d . cos θ, A resposta é zero. Embora o operário exerça uma força em módulo igual ao peso do saco de cimento, que é de 500 N, essa força é na vertical, enquanto seu deslocamento é na horizontal, ou seja, o ângulo entre a força e o deslocamento é 90°. Quando a força e o deslocamento formam um ângulo igual a 90°, o trabalho realizado por essa força é nulo. Veja:

 T = F . d . cos θ

θ = 90°, logo cos 90° = 0, então T = 0

T = 500 . 20 . 0

T = 0

4) Um objeto é empurrado por uma força de intensidade 100 N que forma um ângulo de 60º com a horizontal. Sabendo que a velocidade do objeto durante a atuação da força é de 2 m/s, determine a potência média desenvolvida.

Resoluçaõ:

F = 50N

v = 2m/s

cos 60° = 0,5

P = ?

Sabemos que P  = E/Δt, a energia, nesse caso, é o trabalho realizado pela força. Assim, temos:

E = T

E = F . d . cos 60°

E = 100 . 2 . 0,5  ( 2m/s significa 2m a cada segundo, assim d = 2m e o tempo é t = 1s )

E = 100J

P = E/Δt

P = 100/1

P = 100W

5) Calcule a energia potencial elástica armazenada em uma mola, cuja constante elástica é 100 N/m, que está comprimida, apresentando uma deformação de 45 cm.

Resolução:

Epe = ?

K = 100N/m

x = 45cm = 0,45m

Epe = K . x²

             2

Epe = 100 . 0,45²

                 2

Epe = 100 . 0,2025

                  2

Epe = 20,25

              2

Epe = 10,125J

Agora faça os exercícios.

Exercícios.

1) Um operário da construção civil levanta um saco de cimento de 50Kg a uma altura de 1,20m. Adotando a aceleração da gravidade igual a 10m/s², podemos afirmar que a energia potencial gravitacional adquirida pelo saco de cimento foi de:

a) 600J

b) 60J

c) 6000J

d) 560J

e) 56J

2) Um veículo de 1200Kg que se desloca com velocidade constante de 72Km/h possui uma energia cinética de:

a) 3,11 . 10⁶J

b) 4,8 . 10⁵J

c) 2,4 . 10⁵J

d) 2,4 . 10⁶J

e) 4,8 . 10 ⁶J

3) Uma mola é deslocada 10cm da sua posição de equilíbrio; sendo a constante elástica desta mola equivalente à 50N/m, determine a energia potencial elástica associada a esta mola em razão desta deformação.

a) 2,5J

b) 25J

c) 2500J

d) 0,25J

e) 250J

4) Um halterofilista eleva um conjunto de barra e anilhas cuja massa total é de 200 kg. Inicialmente, o conjunto estava em equilíbrio estático, apoiado sobre a superfície do piso. O halterofilista eleva o conjunto até uma altura de dois metros em relação ao piso. O movimento de elevação do conjunto foi realizado em um intervalo de tempo de quatro segundos. Considere o módulo da aceleração gravitacional terrestre como 10 m/s². A potência média gasta pelo halterofilista para elevar o conjunto de barra e halteres foi de:

a) 0,5 .10³ watts

b) 10² watts

c) 4 . 10³ watts

d) 2 . 10³ watts

e) 10³ watts

5) Uma mala é puxada sobre um plano horizontal por uma força de 50 N. Essa força forma ângulo de 37° com o deslocamento do corpo, que é de 4 m. Calcule o trabalho da força. Dado: cos 37° = 0,8.

a) 1,6 . 10³J

b) 1,6 . 10²J

c) 16J

d) 1,6J

e) 1,6 . 10⁴J