Aula 2 -2º Bimestre - Múltiplos e Potenciação 6E

Bom dia Alunos ,

Segue nosso conteúdo da aula da semana .


Aula 2 -2º Bimestre - Múltiplos e Potenciação 6E

Atividades a serem realizadas durante a semana:

1. Assistam  as aulas apresentado na Central de mídias e façam as anotações em seu caderno pertinentes a  nossa aula de matemática ;.
2. Fazer a leitura do livro a partir da pagina  112 sobre divisores e múltiplos de um números  natural;
3. Resolver os exercícios da pagina 114 do livro didático
4. Resolver os exercícios sobre as propriedades da potenciação enviados abaixo:

Texto complementar sobre potenciação para que vocês possam aprender melhor :

Podemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 2⁶, onde 2 é a base e 6 o expoente (Leia: dois elevado a sexta potência). Todo número diferente de zero e elevado a zero é um.

A potenciação é uma simplificação da forma de expor uma multiplicação de fatores iguais. Antes de detalhar a potenciação, vamos nos lembrar da adição. Nas séries iniciais, aprendemos a somar e logo vemos que existem formas de melhor expressar somas, como:

a) 2+2+2+2+2+2+2

b) 3+3+3+3+3

c) 4+4+4+4+4+4+4+4+4+4

No item a, se somarmos o número 2 com ele mesmo 7 vezes, obteremos o resultado 14. Mas esse resultado poderia ter sido obtido mais rapidamente através do cálculo 2 x 7 = 14. No item b, a soma do número 3 cinco vezes pode ser substituída pela multiplicação de 3 x 5, pois em ambas obtemos o resultado 15. No item c, a soma do número 4 dez vezes pode ser representada pela multiplicação de 4 x 10, que é igual a 40.

Assim como podemos expressar uma soma de fatores iguais através do produto desse fator pela quantidade de vezes que é repetido, nós podemos substituir a multiplicação de termos pela potenciação. Vejamos um exemplo:

3 x 3 = 9

3 x 3 x 3 = 27

3 x 3 x 3 x 3 = 81

Nos três exemplos acima, nós estamos multiplicando apenas o número 3. Vejamos agora como ficaria a multiplicação repetindo o número 3 dez vezes.

3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 59.049

Para simplificar a notação dessas multiplicações, nós podemos utilizar a potenciação. Essa forma de representação foi originalmente criada pelo matemático e filósofo René Descartes (1596 – 1650). Na potenciação, nós representamos apenas uma vez o número que será multiplicado e, acima desse número, colocamos a quantidade de vezes que ele será repetido. Para os exemplos acima, vejamos como ficará a representação através da potenciação:

3 x 3 = 3²

3 x 3 x 3 = 3³

3 x 3 x 3 x 3 = 3⁴

3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 3¹⁰

Podemos generalizar a representação de uma potência da seguinte forma, sejam a e b números racionais, então:

a x a x a x ... x a = a^b
b vezes     

Assim como acontece com as demais operações, os termos de uma potência recebem nomes específicos:

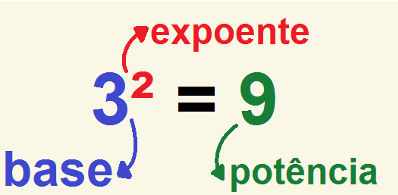
A leitura de uma potência também ocorre de uma forma particular. O exemplo acima é lido como “três elevado a dois”, “três elevado à segunda potência” ou, mais popularmente, “três ao quadrado” ou “três elevado ao quadrado”. Quando se trata do expoente três, também há uma variação específica. A potência pode ser lida como “elevado ao cubo”. Apenas os expoentes dois e três possuem essas variações, a leitura do restante dos expoentes segue uma mesma ideia. Veja os exemplos a seguir:

2⁴ = “dois elevado a quatro” ou “dois elevado à quarta potência”

2⁵ = “dois elevado a cinco” ou “dois elevado à quinta potência”

2⁶ = “dois elevado a seis” ou “dois elevado à sexta potência”

2⁷ = “dois elevado a sete” ou “dois elevado à sétima potência”

2⁸ = “dois elevado a oito” ou “dois elevado à oitava potência”

2⁹ = “dois elevado a nove” ou “dois elevado à nona potência”

2ⁿ = “dois elevado a n” ou “dois elevado à enésima potência”

Em geral, quando nos deparamos com uma potência, precisamos repetir o produto da base quantas vezes indicar o expoente. Mas três regras são facilmente vistas:

1. Quando a base for zero, o resultado da potência será zero.
   0ⁿ = 0
2. Quando o expoente for um, o resultado da potência será exatamente o valor da base.
   a¹ = a
3. Quando o expoente for zero, o resultado da potência será sempre um.
   a⁰ = 1
   

   

   
   

   

Exercícios pagina  114

Responda as questões no caderno

1)    Verifique se 6 e divisor de  e justifique  fazendo a conta :

a)    25

b)    48

c)    72

d)    86

2)    Verifique se 92 e múltiplo de :

a)    4

b)    6

c)    8

d)    23

3)    Entre os elementos do conjunto A = (2,3,5,6,8,9,10), identifique os que são divisores de :

a)    14

b)    18

c)    25

d)    45

e)    54

f)     70

4)    Quais são os divisores de 15 que também são divisores de 257?

5)    Janete e uma moça que tem a idade  correspondente ao maior divisor de 60 sem o ser o próprio 60, qual a idade de Janete ?

6)    Responda com suas palavras o que significa ano bissexto

7)    Efetue as potenciares e, usando < ou > ou =, complete as sentenças para que sejam verdadeiras ou falsas

a)    2⁵____________3³

b)    1²⁰___________10⁰

c)    2³____________3²

d)    1¹____________2¹

8)    Se a potencia de um numero e 256 e a sua base e 4, qual é o seu expoente ?, justifique  com a expressão