Potenciação

Propriedades da potenciação

Considerando as bases a e b números reais, e os números naturais para m e n. Temos as seguintes propriedades:

Qualquer número real elevado ao expoente natural 1 é igual ao próprio número.

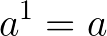
Exemplo: 5¹ = 5

Qualquer número real não-nulo elevado ao expoente natural 0 é igual a 1.

Exemplo: 3⁰ = 1

Qualquer potência que possui na base o número 1 é igual a 1.

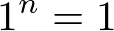
Exemplo: 1¹⁰⁰ = 1

Qualquer potência que tem na base o número 10, o resultado é o número 1 seguido da quantidade de zeros, de acordo com o valor do expoente.

Exemplo: 10⁵ = 100000

Veja que a quantidade de zeros foi definida pelo expoente 5.

Um potência com expoente negativo indica que temos uma inversão entre o numerador com o denominador.

Veja que a potência foi para o denominador sem o sinal, e o numerador é representado pelo número 1 (oculto) do denominador.

Uma potência negativa no denominador é equivalente ao numerador vezes o denominador com o sinal da potência trocado.

Exemplo:

e

No primeiro caso o 1 (um) pode ser omitido porque não altera o valor do produto, 1 x 5² = 5² = 25.

Propriedades operatórias da potenciação

É importante conhecer as propriedades operatórias para auxiliar e simplificar os cálculos envolvendo potenciação.

Produto de potências de mesma base

Ao multiplicar duas ou mais potências de mesma base, devemos proceder da seguinte forma: conservar a base e somar os expoentes.

• a^m.aⁿ = a^{m + n}

Exemplo: 5².5³ = 5^{2 + 3}

Divisão de potências de mesma base

Ao dividirmos potências não-nulas de mesma base, devemos proceder da seguinte forma: conservar a base e subtrair os expoentes.

Exemplo:

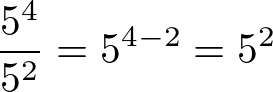
Base negativa e expoente ímpar

Quando a base é negativa e o expoente é ímpar o resultado será negativo, veja o jogo de sinais em subtração.

Exemplo: (-2)³ = -8

Base negativa e expoente par

Quando a base é negativa e o expoente é par o resultado é positivo, veja o jogo de sinais em subtração.

Exemplo: (-5)² = 25

  
De acordo  com os exemplos acima, resolver os exercícios  abaixo:

As potências (-2)4 e -24 são iguais ou diferentes? E qual o resultado?

02 - Calcular: 2³; (-2)³; ; -2³

03 -  Calcular: (0,2)⁴; (0,1)³

04 - Calcular: 2^-3; (-2)^-3; -2^-3

05 -  O valor da expressão (-1)⁰ + (-6) : (-2) – 2⁴é:

a) 20
b) -12
c) 19,5
d) 12
e) 10

Caderno do aluno 3°BIMESTRE 

06- Resolver as atividades

       2, 3, 4, 5  6 e 7.   páginas  6 e 7

Deverão ser respondidas e em enviadas para o e-mail : 

mariaaparecidamagalhaes@prof.educacao.sp.gov.br, 

Identificação do aluno: nome, turma e série. 

A data prevista para entrega é dia 19/08/2020.